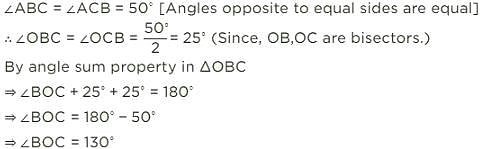Courses

Test: Angles Sum Property A Triangle


15 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Angles Sum Property A Triangle


Description
This mock test of Test: Angles Sum Property A Triangle for Class 9 helps you for every Class 9 entrance exam. This contains 15 Multiple Choice Questions for Class 9 Test: Angles Sum Property A Triangle (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Angles Sum Property A Triangle quiz give you a good mix of easy questions and tough questions. Class 9 students definitely take this Test: Angles Sum Property A Triangle exercise for a better result in the exam. You can find other Test: Angles Sum Property A Triangle extra questions, long questions & short questions for Class 9 on EduRev as well by searching above.
QUESTION: 1

An exterior angle of triangle is 80° and the interior opposite angles are in the ratio 1:3. Measure of each interior opposite angle is:​

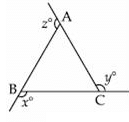
Solution: We know that,ext. angle=into.opp angle1+into.opp angle2let the common factor in the ratio be x.then Angle are x and 3xx +3×=804× =80×=203×=60 the answer is option D.
QUESTION: 2

In fig. if x°, y° and z° are exterior angles of ΔABC, then x° + y° + z° is:

Solution:
QUESTION: 3

The angles of a triangle are in the ratio 2 : 3 : 4. The angles, in order, are :​

Solution:
QUESTION: 4

The angles of a triangle are in the ratio 2:3:4.So, the degree measures of the angles are​
Solution:
QUESTION: 5

The value of x in the given figure is
Solution:
QUESTION: 6

In ΔABC fig., ∠x + ∠y + ∠z is equal to:
Solution: Sum of exterior angles of a triangle is always 360
QUESTION: 7

The measure of angle a in the figure below is :
Solution:
QUESTION: 8

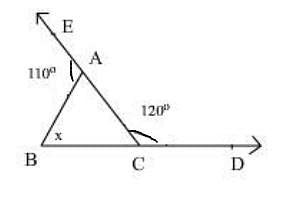
In fig., in ΔABC, AB = AC. The value of x is:
Solution: AB=AC so angle. c = angle b in tri. abc .. now using angle sum property we'll get that angle B and C = 50degree each .. now, angle C + x =180 degree. [ linear pair] 50deg. + x =180 deg. x= 130 deg. Ans.
QUESTION: 9

The sum of two angles of a triangle is 116° and their difference is 24°. The measure of each angle of the triangle is​
Solution: Let,first angle of triangle=X second angle of triangle=x-24 acc.to.ques 116-x=x-24 116+24=X+X 140=2x 140/2=X 70=x Now,X=70 x-24=70-24=46 Now,thrid angle of triangle=x 70+46+x=180(sum of angles of triangle) 116+x=180 x=180-116 x=64 Now,first angle=70 degree second angle=46 and third angle=64degree.
QUESTION: 10

The three angles of a triangle, one is twice the smallest and another one is thrice the smallest.find the angles
Solution:
QUESTION: 11

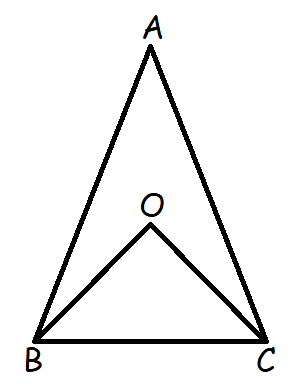
The bisectors of the base angles of an isosceles triangle ABC, with AB = AC, meet at O. If ∠B = ∠C = 50°. What is the measure of angle O?
Solution: The answer is b ,because in triangle OBC, angle OBC =25 degree, OCB =25degee and angle O is not given so, sum of all the angles will be 50 + angle O = 180 degreeangle O = 180-50angle O =130 degree
QUESTION: 12

In a triangle ABC if ∠A = 53° and ∠C = 44° then the value of ∠B is:
Solution: B=180-(A+C) B=180-53+44 B=180-97 B=83
QUESTION: 13

Find the measure of angle marked e in the figure below:
Solution: D+e=180(angles on linear pair),but d=30(vertically opposite angles),30+e=180,e=180-30,e=150
QUESTION: 14

If in triangle DEF, the greatest angle is twice the smallest and the third angle is 20 degrees more than the smallest, what are the angles?​
Solution:
QUESTION: 15

If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the ____ interior opposite angles.
Solution: An exterior angle of a triangle is formed, when a side of a triangle is produced. The measure of any exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles. The sum of the three angles of a triangle is 180degree.

Recommended Content

Recommended Tests

Related tests

Follow Us
© 2015-20 EduRev