Test: Cyclic Quadrilaterals - Class 9 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Cyclic Quadrilaterals
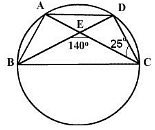
A, B, C and D are four points on a circle. AC and BD intersect at E such that angle BEC =140° and angle ECD = 25°, then angle BAC is
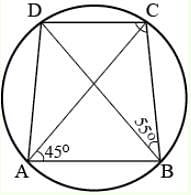
ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If angle DBC = 55° and angle BAC = 45°, the measure of angle BCD is

In the figure, triangle ABC is an isosceles triangle with AB = AC and measure of angle ABC = 50°. Then the measure of angle BDC and angle BEC will be
In the figure, quadrilateral PQRS is cyclic. If ∠P = 80°, then ∠R =
If AB = 12 cm, BC = 16 cm and AB ⊥ BC, then radius of the circle passing through A,B and C is
In the figure, ABC is an equilateral triangle. Measure of angle BEC is
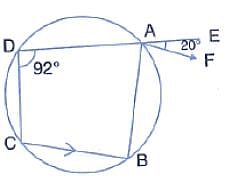
In the figure, ABCD is a cyclic quadrilateral. AE is drawn parallel to CD and BA is produced to point F. If angle ABC = 92°, angle FAE = 20°; then angle BCD will be
In the figure, angle BAD = 75°, angle DCF = x and angle DEF = y.The values of x and y are
If the sum of a pair of opposite angles of a quadrilateral is 180o, the quadrilateral is:
In the figure, O is the centre of the circle. The measure of angle CBD is
ABCD is a cyclic quadrilateral in a circle with centre O. If angle ADC = 130°; then angle BAC is
ABC is an isosceles triangle in which AB = AC. If D and E are the mid points of AB and AC respectively, then the points D, B, C and E are
|
44 videos|412 docs|54 tests
|