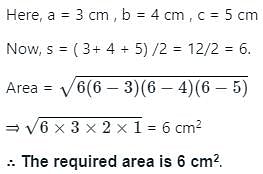Test: Heron's Formula- 1 - Class 9 MCQ
25 Questions MCQ Test Online MCQ Tests for Class 9 - Test: Heron's Formula- 1
The area of a triangle with base 8 cm and height 10 cm is
The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is
The cost of turfing a triangular field at the rate of Rs. 45 per 100 m2 is Rs. 900. If the double the base of the triangle is 5 times its height, then its height is
The area of the the triangle having sides 1 m, 2 m and 2 m is :
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be
The area of a triangle whose sides are 12 cm, 16 cm and 20 cm is
The difference of semi-perimeter and the sides of △ABC are 8, 7 and 5 cm respectively. Its semi-perimeter ‘s’ is
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is
The sides of a triangular flower bed are 5 m, 8 m and 11 m. the area of the flower bed is
A triangle ABC in which AB = AC = 4 cm and ∠A = 90o, has an area of
The perimeter and area of a triangle whose sides are of lengths 3 cm, 4 cm and 5 cm respectively are
The perimeter of a rhombus is 20 cm. One of its diagonals is 8 cm. Then area of the rhombus is
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is
The length of the sides of a triangle are 5 cm, 7 cm and 8 cm. Area of the triangle is :
If the side of an equilateral triangle is 4 cm, then its area is
The area of a triangle whose sides are 15 cm, 8 cm and 19 cm is
If one side and one diagonal of a rhombus and 20 m and 24 m, then its area =
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is
If the perimeter of an equilateral triangle is 24 m, then its area is
Each of the equal sides of an isosceles triangle is 2 cm greater than its height. If the base of the triangle is 12 cm, then its area is
The product of difference of semi-perimeter and respective sides of △ABC are given as 13200 m3. The area of △ABC, if its semi-perimeter is 132m, is given by
The area of equilateral triangle of side ‘a’ is 4√3 cm2. Its height is given by
The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be :
|
5 docs|314 tests
|