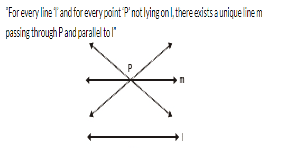Courses

Test: Introduction To Euclid's Geometry - 2


25 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Introduction To Euclid's Geometry - 2


Description
This mock test of Test: Introduction To Euclid's Geometry - 2 for Class 9 helps you for every Class 9 entrance exam. This contains 25 Multiple Choice Questions for Class 9 Test: Introduction To Euclid's Geometry - 2 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Introduction To Euclid's Geometry - 2 quiz give you a good mix of easy questions and tough questions. Class 9 students definitely take this Test: Introduction To Euclid's Geometry - 2 exercise for a better result in the exam. You can find other Test: Introduction To Euclid's Geometry - 2 extra questions, long questions & short questions for Class 9 on EduRev as well by searching above.
QUESTION: 1

Euclid's Axiom 1 is :

Solution:
QUESTION: 2

Euclid's Axiom 5 is :

Solution:
QUESTION: 3

Euclid's Postulate 1 is :

Solution:
QUESTION: 4

Two distinct lines :
Solution:
QUESTION: 5

A line segment when extended indefinitely in one direction is called .................
Solution:
QUESTION: 6

Two distinct points in a plane determine .................
Solution:
QUESTION: 7

For every line l and for every point P not lying on it there exist a unique line which passes through P and is
................. to l.
Solution:

QUESTION: 8

If a straight line falling in two straight line make the interior angles on the same side of it taken together, then two straight lines if produced indefinitely, meet on that side on which the sum of angles are ................. 2 right angles.
Solution: If a straight line falling on two straight lines makes the interior angles on the same side of it, taken together less than two right angles, then the the two straight lines if produced indefinitely, meet on that side on which the sum of angles is taken together less than two right angles.
QUESTION: 9

Which of the following statement is true :
Solution:
QUESTION: 10

Two lines are intersecting, if they have :
Solution:
QUESTION: 11

Three basic terms in geometry namely a point, line and plane are ................. terms.
Solution:
QUESTION: 12

If two circles are equal, then their radii are .................
Solution:
QUESTION: 13

How many lines can pass through a given point ?
Solution:
QUESTION: 14

Which of the following statement is true ?
Solution:
QUESTION: 15

Three or more lines are called concurrent lines if they pass through ................. point.
Solution:
QUESTION: 16

The three steps from solids to points are
Solution: Firstly, a cube is a solid. It has 6 surfaces. After the breakdown a solid cube we get 6 surfaces. That is if we take 6 identical Squares of paper, and join them together in a particular order we get a cube.Now when we take one of its surfaces, we see that it is made up of 4 lines. That is for example if we take four matches and join their ends together to form a square, we get one surface of the cube. If we keep adding matchsticks, we get a cube.Now if we take one line which is one matchstick, we see that it is made of particles of wood joined together is a straight order to form a line. That is Many points come together to form a line.Thus breaking down a solid to its components, we can write that:-Solids are made of surfaces.Surfaces are made of lines.Lines are made of points.Therefore --- Solids-> Surfaces-> Lines-> Points.
QUESTION: 17

The number of dimension, a point has
Solution:
QUESTION: 18

The number of dimensions, a line has
Solution:
QUESTION: 19

The number of dimensions, a surface has
Solution:
QUESTION: 20

The number of dimensions, a solid has
Solution:
QUESTION: 21

Euclid divided his famous treatise “The Elements” into
Solution:
QUESTION: 22

The total number of propositions in the Euclid’s Elements are
Solution:

In the thirteen books that comprise Euclid's Elements there is a total of 465 propositions.

QUESTION: 23

The boundaries of surfaces are
Solution:

A surface may not have a boundary.A point is on the boundary if and only if any neighborhood of the point contains some points in the set and some not in the set. 
An entire plane does not have a boundary and a sphere (the surface of a ball) does not have a boundary. Both of those, by the way, are examples of a basic theorem in topology- the boundary of a boundary is always the empty set.
boundary points look like (0,0) looks in relation to the set of those (x,y) where y is non negative. i.e. it is on the edge of that set of points.

QUESTION: 24

The boundaries of solids are
Solution:
QUESTION: 25

A pyramid is a solid figure, the base of which is
Solution:

Recommended Content

Recommended Tests

Related tests
Follow Us
© EduRev