Test: Lines And Angles- 2 - Class 9 MCQ
15 Questions MCQ Test - Test: Lines And Angles- 2
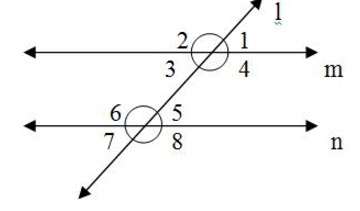
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –
If two angles are supplementary and the larger is 200 less then three times the smaller, then the angles are :-
In a right-angled triangle where angle A = 90° and AB = AC. What are the values of angle B?
An exterior angle of a triangle is 800 and the interior opposite angles are in the ratio 1 : 3. Measure of each interior opposite angle is :
In figure, AB and CD are parallel to each other. The value of x is :
In the adjoining figure, m ║ n. If ∠a : ∠b = 2 : 3, then the measure of ∠h is –
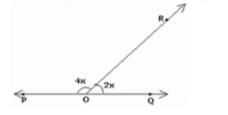
In the figure, POQ is a line, ∠POR = 4x and ∠QOR = 2x. Find the value of x.
In the figure, a is greater than b by one third of a right angle. Find the values of a and b.
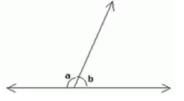
In two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 5 : 4, then the smaller of the two angles is :
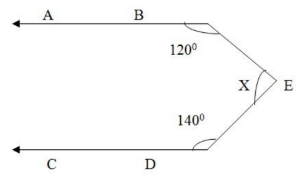
In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-
Find the angle if six times of its complement 12° less than twice of its supplement?