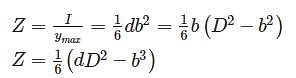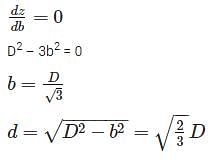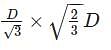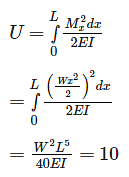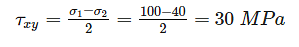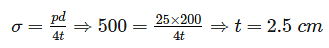Strength of Materials - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test SSC JE Mechanical Mock Test Series 2025 - Strength of Materials - 2
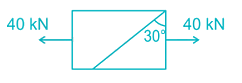
A rectangular bar of cross sectional area 10000 mm2 is subjected to an axial load of 40 kN. Determine the normal stress on the section which is inclined at an angle of 30° with normal cross-section of the bar.

For a thin spherical shell subjected to internal pressure, the ratio of volumetric strain to diametrical strain is _____.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
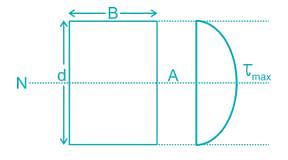
For a rectangular section, the ratio of the maximum and average shear stresses is
Young’s modulus of elasticity is defined as the ratio of which of the following?
For beams of uniform strength, if depth is constant, then
According to maximum shear stress direction, at what ratio of maximum shear stress to yield stress of material does the yielding of material takes place?
A cantilever beam is deflected by δ due to load P. If length of beam is doubled, the deflection compared to earlier case will be changed by a factor of:
If a shaft turns at 150 rpm under a torque of 1500 Nm, then power transmitted is
A closed coil helical spring has 25 coils. If five coils of this springs are removed by cutting, the stiffness of the modified spring will
A tensile test is performed on a round bar. After fracture it has been found that the diameter remains approximately same at fracture. The material under test was
A rod of dimension 20 mm x 20 mm is carrying an axial tensile load of 10 kN. The tensile stress developed is ________.
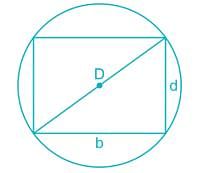
A circular log of timber has diameter D. What will be the dimensions of the strongest rectangular section one can cut form this?
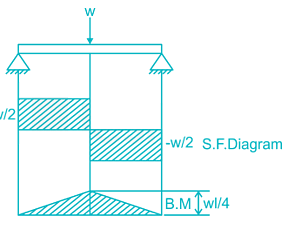
The correct shear force diagram for the cantilever beam with uniformly distributed load over the whole length of the beam is -
A cantilever beam 2 m in length is subjected to uniform load of 5 kN/m. If E = 200 GPa and I = 1000 cm, The strain energy stored is _____J
Effective length of a column effectively held in position and restrained in direction at one end but neither held in position nor restrained in direction at the other end is
If the principle stresses on a plane stress problem are S1 = 100 MPa and S2 = 40 MPa then the magnitude of maximum shear stress (MPa) will be:
A spherical vessel with an inside diameter of 2 m is made of material having an allowable stress in tension of 500 kg/cm2. The thickness of a shell to with stand a pressure of 25 kg/cm2 should be:
The bending moment diagram of a simply supported beam with a point load at centre is:
At a point in beam, the principle stresses are 100 N/mm2 and 50 N/mm2. The stress in x-direction is 65 N/mm2. The stress in y-direction will be
|
3 videos|1 docs|55 tests
|
|
3 videos|1 docs|55 tests
|



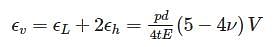
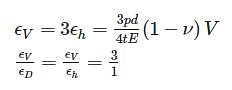
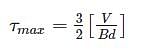
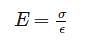
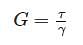
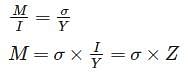
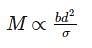

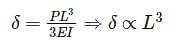
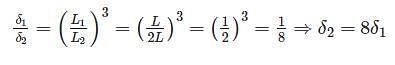

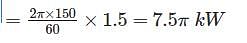
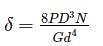
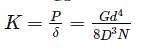
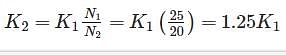
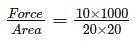 =25N/mm2=25MPa$
=25N/mm2=25MPa$