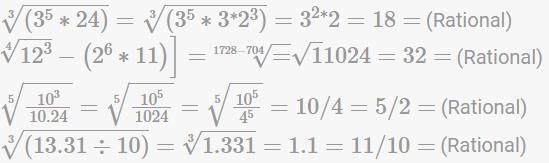RRB JE CE (CBT I) Mock Test- 2 - Civil Engineering (CE) MCQ
30 Questions MCQ Test RRB JE Mock Test Series for Civil Engineering (CE) 2025 - RRB JE CE (CBT I) Mock Test- 2
In a school, 1000 chocolates were distributed in such a way that each student gets chocolates equal to 10% of the total students. Find the number of chocolates that each student gets
If the cost price of 12 pen is same as the selling price of 15 pen. What is the percentage of gain or loss?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The following table represents marks obtained by four students in five subjects and maximum marks of each subject.
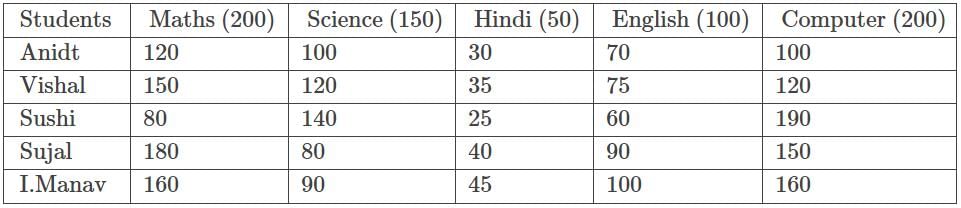
Q. Find the respective ratio of overall percentage of marks obtained by Ankil in all the five subjects and overall percentage of marks obtained by Sulal in all the five subjects.

Area of rhombus is (7 + 6.5√5) cm2 and length of its one diagonal is (3 + 2√5) cm, then what is the length of its second diagonal?
Solve the following expression: (∛42875 ÷ √49) + (152 - 21 x 10) - √625.
A set of 7 pipes can fill 70% of a vessel in 7 minutes. Another set of 5 pipes can fill 2/5th of the vessel in 5 minutes. A third set of 10 pipes can empty 1/3rd of the tank in 10 minutes. How much time (in minutes) will it take to fill the entire tank if all the pipes are opened at the same time?
If an article is sold for a gain of 7% instead of selling it at a loss of 13%, a trader gets Rs.1080 more. What is the selling price of the article, when the article is sold at a profit of 25%?
There are total 10 students whose marks in an exam are 45, 65, 56, (P + 16), (2P + 3), 78, 24, (4P - 8), 44 and 48 respectively and mean marks of first 5 students is 49, then what is mean marks of last 5 students?
Select the odd one out: (6 x 10-3), √[(52 + 11) x 10-6], (0.06 ÷ 102) and √0.000036.
There is a fraction such that if we add 11/30 to it then it gets reverted. Further if we subtract 1 from numerator then the fraction becomes 2/3. What is the fraction?
How many among the following numbers are Irrational number: 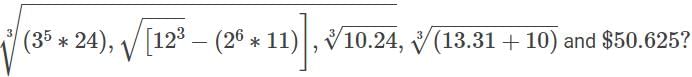
Ramesh and Suresh invested same amount of money in two banks for 2 years which offer interest at the same rate, but Ramesh invested in a bank which offers compound interest and Suresh invested in a bank which offers simple interest. After two years Ramesh got Rs. 525 as interest and Suresh got Rs. 500 as interest. What is the rate of interest offered by the banks?
Line graph given below shows the total number of presence of employees in two different companies P and Q on five different working days from Monday to Friday.
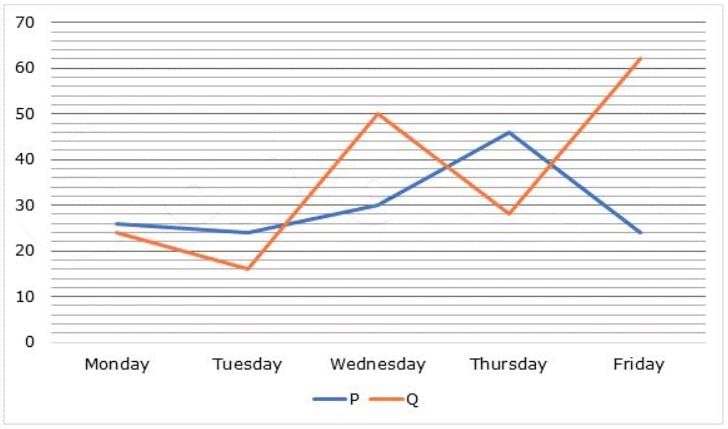
Q. What is the sum of the average number of presence of employees in company P and average number of presence of employees in company Q on all the five working days?
If [(0.09)2 x (0.3)8 x (0.027) x 1012] / [312 x (0.3)x] = 1, then what is the value of x?
In one revolution, the object travels______ distance.
Sita buys a parker pen at Rs. 100 and sell it to Geeta at Rs. 120. Geeta sells this pen to Radha at a price of Rs. 80. Radha sells it back to Sita at Rs. 90. Sita sells it to Roma at Rs. 150. What is Sita's profit/loss %?
Mahesh is travelling at a distance of 1200 km in Japan by Bullet train. Due to some technical fault in the engine of the train, speed of the train was reduced by 100 km/hr thus overall time of his journey increased by 24 minutes. What was the normal speed of the bullet train?
If 4x - 1/3x = 9, then what is the value of (144x4 - 1)/(27x2 + 2x)?
What is the simplified value of (cos3 x/sin x) + (cos2 x.cot3 x)?
If 25% of (A + B) is 30% of (A - B), then B is what percent of A?
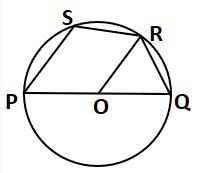
What is the ∠SRO if O is the centre of circle, ∠SPO = 550 and ∠POR = 1150
A number 135 is split into three parts in such a way that all the three parts are in increasing Arithmetic Progression. The Product of the two largest parts is 2160, then what is the ratio of the smallest part to the highest part?
Simplify the value of 3[{1/(√9 - √8)} - {1/(√9 + √8)}] + (2 - 3√2)2.
There are 7 students in a class whose weights are: 54 kg, 45 kg, 48 kg, A kg, 42 kg, 50 kg and 55 kg. If the mean of their weights is 49 kg, then what is the median of their weights?
The LCM of two numbers is 2376, and their HCF is 22. Find their difference, if the sum of numbers is 682.
60 liters of first mixture of milk and water is mixed with another 40 liters mixture of milk and water. After mixing the mixture, the mixture is sold at the cost of pure milk, then what is the percent profit gained if the ratio of milk to water in the first and second mixture is 7: 5 and 3: 5, respectively? Given below are the steps involved. Arrange them in sequential order.
(A) Amount of milk and water in first mixture is 60 x (7/12) = 35 liters and 60 x (5/12) = 25 liters respectively.
(B) Total amount of milk and water is final mixture is (35 + 15) = 50 liters and (25 + 25) = 50 liters respectively.
(C) Percent profit earned = [(100 - 50)/50] x 100 = 100%
(D) Amount of milk and water in second mixture is 40 x (3/8) = 15 liters and 40 x (5/8) = 25 litres respectively.
(E) Cost price of final mixture = 50 x 1 = 50 and selling price of final mixture = 100 x 1 = 100
If cosec θ = x + 1/4x, then the value of cosec θ + cot θ is:
At present, the sum of ages of R and K is 63 years. The ratio of their ages after 7 years will be 7: 4 , what is the present age of R?
If 5 girls can embroider a dress in 9 days, then the number of days taken by 3 girls will be _____.
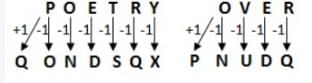
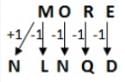
In a certain code language, ‘POETRY’ is written as ‘QONDSQX’ and ‘OVER’ is written as ‘PNUDQ.’ How is ‘MORE’ written in that code language?