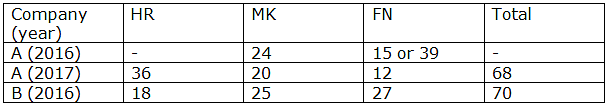Test: Quantitative Aptitude - 1 - Bank Exams MCQ
20 Questions MCQ Test RBI Grade B Mock Test Series & Past Year Papers 2024 - Test: Quantitative Aptitude - 1
Directioons: In each of the following question three or more statements is given. You are expected to decide which of the following statement or pair of statement is sufficient to answer the question.
Q. 6 years ago, age of father of Roma 14 years more than her only one brother and only one sister. Find the age of Sister of Roma after 12 years?
Statement I. Roma is 20 years younger than her father and her present age of 116.66% of her brother.
Statement II. 4 years ago, age of brother is 166.66% of Sister
Statement III. 8 years hence, Age of Father is same as sum of ages of her brother and Sister.
Read the following information carefully and answer the questions based on it.
Article P sold at 35% profit and Q at 20% profit, MRP of P is 92% more that of Q. Selling price of Q is 58.33% less than that of P. Article P sold after discount of (M – 15) % and Q at discount of (N +20) %. N is half of M.
Q. A retailer cheats whole seller, buys M% extra quantity and, cheats customer by giving N% less quantity. He claims no profit no loss to customer, who don’t know about cheating, fin d his actual profit %.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Quantity I. A and B entered into a partnership with initial investments of Rs. 3200 and Rs. 5000 respectively. After 6 months A increased his investment by 60% while B increased his investment by 40%. At the end of 1.5 years, difference in profit of A and B is Rs. 3336 then find the total profit earned by A and B together.
Quantity II. If difference between total surface area and curved surface area of cylinder is 7776 cm2. Find 30% of volume of cylinder, if height is 20 cm less than radius. Only numerical value.
Directions: Read the following information carefully and answer the questions based on it.
Article P sold at 35% profit and Q at 20% profit, MRP of P is 92% more that of Q. Selling price of Q is 58.33% less than that of P. Article P sold after discount of (M – 15) % and Q at discount of (N +20) %. N is half of M.
Q. If cost price of both articles together is Rs. 3760, then which of the following can be the possible value of (2M + 3N).
I. 87.5% of difference between cost price of P and twice of cost price of Q
II. 148 less than HCF of (Selling price of P, selling price of Q)
III. Rs. 20 more than profit earned on article R, whose cost price is same as that of Q, and having same markup %
P, Q, and invested in a business. Initial investment of P is 66.66% as that of Q, while initial investment of R is 275% more than that of P. P and Q started together and after 8 months P invested 50% more to his investment, Q invested 66.66% more to his investment and R joined them. If initial investment of Q is Rs. 12000, and at the end of year total profit is 1.7 lakhs. They donated 25% of profit for education of children.
M = Difference between profit share of P and Q
N = (2500 + difference between profit share of Q and R)
Q. Find which of the following option is true.
Directions: Read the following information carefully and answer the questions based on it.
There are two companies A and B. Each company have three departments – HR, Marketing (MK) and Finance (FN).
- Employees in MK of company A (2016) were 2(a + c), which is 6 more than employees in HR of company B (2016), which in turn 28% less than employees in MK of company B (2016).
- Employees in HR of company A (2017) is 24 more than that of employees in FN of same company in same year. Employees in MK of company A (2017) were (3c – a/5), while employees in FN of company A (2017) were 2(a + 1).
- Employees in FN of company B (2016) is 50% more than employees in HR of same company in same year, while difference between employees in FN of company A (2016) and B (2016) is same as number of employees in FN of company A (2017)
- a, b, c are positive integers. Where ‘a’ is prime number more than 3, while ‘b’ is an odd composite number more than 4. Sum of a and b is less than 20, and c is 50% of sum of a and b.
- In company A (2016), number of employees is finance is less than employees in other two department in same year and same company.
Q. Find Minimum possible number of employees in company A in 2016?
Directions: Read the following information carefully and answer the questions based on it.
There are two companies A and B. Each company have three departments – HR, Marketing (MK) and Finance (FN).
- Employees in MK of company A (2016) were 2(a + c), which is 6 more than employees in HR of company B (2016), which in turn 28% less than employees in MK of company B (2016).
- Employees in HR of company A (2017) is 24 more than that of employees in FN of same company in same year. Employees in MK of company A (2017) were (3c – a/5), while employees in FN of company A (2017) were 2(a + 1).
- Employees in FN of company B (2016) is 50% more than employees in HR of same company in same year, while difference between employees in FN of company A (2016) and B (2016) is same as number of employees in FN of company A (2017)
- a, b, c are positive integers. Where ‘a’ is prime number more than 3, while ‘b’ is an odd composite number more than 4. Sum of a and b is less than 20, and c is 50% of sum of a and b.
- In company A (2016), number of employees is finance is less than employees in other two department in same year and same company.
Q. If number of employees in FN of company A in 2016 is more than 15, then find minimum possible difference between number of employees in company A in 2016 and in 2017?
Directions: Read the following information carefully and answer the questions based on it.
There are two companies A and B. Each company have three departments – HR, Marketing (MK) and Finance (FN).
- Employees in MK of company A (2016) were 2(a + c), which is 6 more than employees in HR of company B (2016), which in turn 28% less than employees in MK of company B (2016).
- Employees in HR of company A (2017) is 24 more than that of employees in FN of same company in same year. Employees in MK of company A (2017) were (3c – a/5), while employees in FN of company A (2017) were 2(a + 1).
- Employees in FN of company B (2016) is 50% more than employees in HR of same company in same year, while difference between employees in FN of company A (2016) and B (2016) is same as number of employees in FN of company A (2017)
- a, b, c are positive integers. Where ‘a’ is prime number more than 3, while ‘b’ is an odd composite number more than 4. Sum of a and b is less than 20, and c is 50% of sum of a and b.
- In company A (2016), number of employees is finance is less than employees in other two department in same year and same company.
Q. Find minimum possible difference between number of employees in FN of company A and B in 2016?
Directions: Read the following information carefully and answer the questions based on it.
There are two companies A and B. Each company have three departments – HR, Marketing (MK) and Finance (FN).
- Employees in MK of company A (2016) were 2(a + c), which is 6 more than employees in HR of company B (2016), which in turn 28% less than employees in MK of company B (2016).
- Employees in HR of company A (2017) is 24 more than that of employees in FN of same company in same year. Employees in MK of company A (2017) were (3c – a/5), while employees in FN of company A (2017) were 2(a + 1).
- Employees in FN of company B (2016) is 50% more than employees in HR of same company in same year, while difference between employees in FN of company A (2016) and B (2016) is same as number of employees in FN of company A (2017)
- a, b, c are positive integers. Where ‘a’ is prime number more than 3, while ‘b’ is an odd composite number more than 4. Sum of a and b is less than 20, and c is 50% of sum of a and b.
- In company A (2016), number of employees is finance is less than employees in other two department in same year and same company.
Q. Find total number of employees in company B in 2016?
Directions: Read the following information carefully and answer the questions based on it.
There are two companies A and B. Each company have three departments – HR, Marketing (MK) and Finance (FN).
- Employees in MK of company A (2016) were 2(a + c), which is 6 more than employees in HR of company B (2016), which in turn 28% less than employees in MK of company B (2016).
- Employees in HR of company A (2017) is 24 more than that of employees in FN of same company in same year. Employees in MK of company A (2017) were (3c – a/5), while employees in FN of company A (2017) were 2(a + 1).
- Employees in FN of company B (2016) is 50% more than employees in HR of same company in same year, while difference between employees in FN of company A (2016) and B (2016) is same as number of employees in FN of company A (2017)
- a, b, c are positive integers. Where ‘a’ is prime number more than 3, while ‘b’ is an odd composite number more than 4. Sum of a and b is less than 20, and c is 50% of sum of a and b.
- In company A (2016), number of employees is finance is less than employees in other two department in same year and same company.
Q. Which of the following can be the maximum possible sum of number of employees in 2016 in both companies together?
Directions: Read the following information carefully and answer the questions based on it.
Equation 1. 6P2 – 19P – (M2 – 4) = 0, M is positive integer
Equation 2. 4(Z – 4Y)2 + 4Y2 + K2 – 4YK = 0
(-7/3) and K is the root of equation 1.
Q. Find M is approx. how much % more or less than K?
Directions: In each of the following question three or more statements is given. You are expected to decide which of the following statement or pair of statement is sufficient to answer the question. Find the Value of D.
Q. A boatman covers a total distance of ‘2D + 160’ km daily. He started from his home daily at fixed time and go to his work place and after that come to home by same route. Speed of river is 4 km/h, and he used different boats on each day. Flow of river is from home to workplace.
Statement I. Speed of boat in still water on Monday is 50% more than that of Wednesday, which is 55.55% less than that on Tuesday.
Statement II. Total traveling time on Wednesday is 128/3 hours.
Statement III. Time taken for return journey on Tuesday is 12.5% less than forward journey on Monday.
Directions: In each of the following question three or more statements is given. You are expected to decide which of the following statement or pair of statement is sufficient to answer the question.
Q. The LCM of two positive integers P and Q is 165. What will be the 50% of HCF of P and Q?
Statement I. 50% of (P – Q) is a multiple 3 less than 12
Statement II. 75% of (P + Q) = 36
Statement III. P2 – 55P + 726 = 0
24, 38, (2P), 98, 148, 214
(P – 11) is the first term of another sequence have same logic as the given sequence find 4th element of later sequence.
Directions: In each of the following question three or more statements is given. You are expected to decide which of the following statement or pair of statement is sufficient to answer the question.
Q. A water tank is cuboidal in shape having dimension (48 cm x 32 cm x 40cm). if there is a leakage in tank, so this leakage emptied the water at the rate of 64 cm3/ second. Two taps T1 and T2 together can fill the tank in 7.5 minutes. Find the time taken by tap T1 to fill the tank.
I. Time taken by tap T3 and T2 together to fill the tank is 10 minutes.
II. time taken by T2 to fill the tank with leakage is 48 minutes.
III. Time taken by T3 to fill the tank which is hemispherical in shape is 2 hours. Volume of hemispherical tank is twice as that of cuboidal tank
Directions: Read the following information carefully and answer the questions based on it.
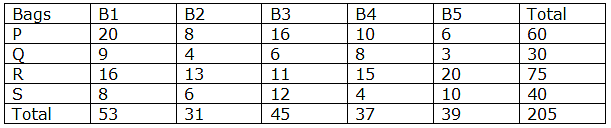
There are four bags – P, Q, R, and S. Each bag contains five type of balls – B1, B2, B3, B4, and B5.
Bag P: Number of B4 balls is 10, which is 2 more than B2. Number of B1 balls in bag P is 5 times of B2 balls in bag Q. Respective ratio of number of B3 and B5 balls is 8:3, and probability of picking a B2 ball from bag is 2/15.
Bag Q: number of B4 and B2 balls respectively is 8 and 4. Number of B1 balls is thrice of B5 balls and total balls in bag is 5 times of B5 balls in bag P. Difference between probability of picking a B1 balls and probability of picking a B5 ball is 1/5.
Bag R: Number of B3 balls is 11, which is 55% of number of B5 balls. Total balls in bag are35 more than bag S, and probability of picking two B4 balls from bag is 7/185. Number of B1 balls is 4 times of number of B4 balls in bag S.
Bag S: Number of B3 balls is 50% more than that of B1, while number of B5 balls are 10. Probability of picking a B2 ball from bag is 3/20, while number of B2 balls is 50% more than B4. Number of B3 balls are 12.
Q. Find probability of picking two B4 balls from bag S?
Directions: Read the following information carefully and answer the questions based on it.
There are four bags – P, Q, R, and S. Each bag contains five type of balls – B1, B2, B3, B4, and B5.
Bag P: Number of B4 balls is 10, which is 2 more than B2. Number of B1 balls in bag P is 5 times of B2 balls in bag Q. Respective ratio of number of B3 and B5 balls is 8:3, and probability of picking a B2 ball from bag is 2/15.
Bag Q: number of B4 and B2 balls respectively is 8 and 4. Number of B1 balls is thrice of B5 balls and total balls in bag is 5 times of B5 balls in bag P. Difference between probability of picking a B1 balls and probability of picking a B5 ball is 1/5.
Bag R: Number of B3 balls is 11, which is 55% of number of B5 balls. Total balls in bag are35 more than bag S, and probability of picking two B4 balls from bag is 7/185. Number of B1 balls is 4 times of number of B4 balls in bag S.
Bag S: Number of B3 balls is 50% more than that of B1, while number of B5 balls are 10. Probability of picking a B2 ball from bag is 3/20, while number of B2 balls is 50% more than B4. Number of B3 balls are 12.
Q. Find the difference between probability of picking a B3 ball and a B5 ball from bag P?
Directions: Read the following information carefully and answer the questions based on it.
There are four bags – P, Q, R, and S. Each bag contains five type of balls – B1, B2, B3, B4, and B5.
Bag P: Number of B4 balls is 10, which is 2 more than B2. Number of B1 balls in bag P is 5 times of B2 balls in bag Q. Respective ratio of number of B3 and B5 balls is 8:3, and probability of picking a B2 ball from bag is 2/15.
Bag Q: number of B4 and B2 balls respectively is 8 and 4. Number of B1 balls is thrice of B5 balls and total balls in bag is 5 times of B5 balls in bag P. Difference between probability of picking a B1 balls and probability of picking a B5 ball is 1/5.
Bag R: Number of B3 balls is 11, which is 55% of number of B5 balls. Total balls in bag are35 more than bag S, and probability of picking two B4 balls from bag is 7/185. Number of B1 balls is 4 times of number of B4 balls in bag S.
Bag S: Number of B3 balls is 50% more than that of B1, while number of B5 balls are 10. Probability of picking a B2 ball from bag is 3/20, while number of B2 balls is 50% more than B4. Number of B3 balls are 12.
Q. Find total number of balls in all four bags together?
Directions: Read the following information carefully and answer the questions based on it.
There are four bags – P, Q, R, and S. Each bag contains five type of balls – B1, B2, B3, B4, and B5.
Bag P: Number of B4 balls is 10, which is 2 more than B2. Number of B1 balls in bag P is 5 times of B2 balls in bag Q. Respective ratio of number of B3 and B5 balls is 8:3, and probability of picking a B2 ball from bag is 2/15.
Bag Q: number of B4 and B2 balls respectively is 8 and 4. Number of B1 balls is thrice of B5 balls and total balls in bag is 5 times of B5 balls in bag P. Difference between probability of picking a B1 balls and probability of picking a B5 ball is 1/5.
Bag R: Number of B3 balls is 11, which is 55% of number of B5 balls. Total balls in bag are35 more than bag S, and probability of picking two B4 balls from bag is 7/185. Number of B1 balls is 4 times of number of B4 balls in bag S.
Bag S: Number of B3 balls is 50% more than that of B1, while number of B5 balls are 10. Probability of picking a B2 ball from bag is 3/20, while number of B2 balls is 50% more than B4. Number of B3 balls are 12.
Q. Find number of B2 balls in bag R?
Directions: Read the following information carefully and answer the questions based on it.
There are four bags – P, Q, R, and S. Each bag contains five type of balls – B1, B2, B3, B4, and B5.
Bag P: Number of B4 balls is 10, which is 2 more than B2. Number of B1 balls in bag P is 5 times of B2 balls in bag Q. Respective ratio of number of B3 and B5 balls is 8:3, and probability of picking a B2 ball from bag is 2/15.
Bag Q: number of B4 and B2 balls respectively is 8 and 4. Number of B1 balls is thrice of B5 balls and total balls in bag is 5 times of B5 balls in bag P. Difference between probability of picking a B1 balls and probability of picking a B5 ball is 1/5.
Bag R: Number of B3 balls is 11, which is 55% of number of B5 balls. Total balls in bag are35 more than bag S, and probability of picking two B4 balls from bag is 7/185. Number of B1 balls is 4 times of number of B4 balls in bag S.
Bag S: Number of B3 balls is 50% more than that of B1, while number of B5 balls are 10. Probability of picking a B2 ball from bag is 3/20, while number of B2 balls is 50% more than B4. Number of B3 balls are 12.
Q. Find the probability of picking two B3 balls from bag Q?
|
114 docs|51 tests
|
|
114 docs|51 tests
|