Test: Quantitative Aptitude - 2 - Bank Exams MCQ
20 Questions MCQ Test RBI Grade B Mock Test Series & Past Year Papers 2024 - Test: Quantitative Aptitude - 2
Directions: Read the following information carefully and answer the questions based on it.
An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.
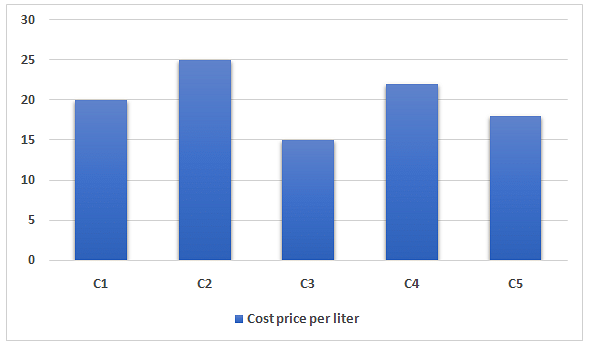
- C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
- Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
- Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.
Q. Which of the following can be the possible cost per liter of Adhesive 2 (AD 2).
I. Rs. 20
II. Rs. 19.25
III. Rs. 20.25
IV. Rs. 19.75

Directions: Read the following information carefully and answer the questions based on it.
An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

- C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
- Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
- Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.
Q. Find cost price per liter of Adhesive 1 (AD1)?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Read the following information carefully and answer the questions based on it.
An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

- C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
- Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
- Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.

Directions: Read the following information carefully and answer the questions based on it.
An adhesive manufacturing company formed adhesives by mixing five chemicals – C1, C2, C3, C4, and C5 in different proportions. Chart given below shows the cost price per liter of these five chemicals.

- C4 formed by mixing C1 and C2 in equal proportion, while C5 formed by mixing C1 and C3 in equal proportion.
- Adhesive 1 (AD1) formed by mixing C2 and C3 in 30% and 70% proportion respectively, while AD2 formed by mixing C4 and C5 in equal proportions.
- Adhesive 3 (AD3) formed by mixing C3 and C4 in equal proportion, while AD 4 formed by mixing C1 and C5 in 2:1.
Q. Find cost price per liter of Adhesive AD4, if company makes maximum profit on selling AD4?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. Find the number of managers joined in 2018?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. In which of the years from 2013 to 2018, did the maximum number of employees join the company?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. Find number of non – managers joined in 2017?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. Find number of employees joined in 2014?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers

It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. Find number of non-Managers left in 2018?
Directions: Read the following information carefully and answer the questions based on it.
The following bar graph shows the number of employees and number of managers working in a company as on 31st December of different years. The company was started in 2010 and from then 1/5thof the employees and 1/4th of managers who joined the company in any year leave the company after exactly two years and no other employee leaves at any other time.
Total employees in company = Managers + Non – Managers
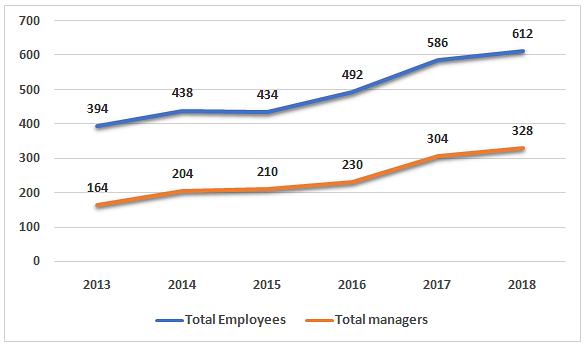
It is also known that 12 employees left in 2016 and 8managers left in 2014. In 2017 as well as 2019, all the employees who left were managers.
Q. Find number of managers left the company from 2014 to 2020?
Directions: Read the following information carefully and answer the questions based on it.
Equation 1. 6P2 – 19P – (M2 – 4) = 0, M is positive integer
Equation 2. 4(Z – 4Y)2 + 4Y2 + K2 – 4YK = 0
(-7/3) and K is the root of equation 1.
Q. Find the value of (Z + Y)?
Directions: Read the following information carefully and answer the questions based on it.
There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.
- Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
- S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
- T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
- R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
- M2 – 64M + 768 = 0
Where distance between Hostel and Manali is 5 times of larger root of given equation.
Q. Who was the second person to reached Manali?
Directions: Read the following information carefully and answer the questions based on it.
There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.
- Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
- S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
- T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
- R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
- M2 – 64M + 768 = 0
Where distance between Hostel and Manali is 5 times of larger root of given equation.
Q. What will be the time when the last person will reach Manali?
Directions: Read the following information carefully and answer the questions based on it.
There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.
- Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
- S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
- T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
- R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
- M2 – 64M + 768 = 0
Where distance between Hostel and Manali is 5 times of larger root of given equation.
Q. If a person who was second last to reached Manali, travel with his original speed for the time in which person who secured rank 2 reached Manali, then find what % of whole journey he covered?
Directions: Read the following information carefully and answer the questions based on it.
There are six friends planning a trip to Manali, all resides in same Hostel somewhere in Delhi. On Monday at 6.30 am, they all started from their hostel, by their own individual cars.
- Speed of P is 50% more than that of R, and Q is 48 km behind Manali when T reached Manali.
- S covered the whole distance in 56 minutes more than the person who was the first to reached Manali.
- T covered half of the journey with speed of K km/h, half of remaining with speed of (K + 5) km/h and rest distance with speed of (K + 20) km/h.
- R covered 60% of whole journey in 3 hours 36 minutes, while initial speed of T is 32 km/h less than S. U was the first person to reached Manali, which covered whole journey with speed of 100 km/h
- M2 – 64M + 768 = 0
Where distance between Hostel and Manali is 5 times of larger root of given equation.
Q. If P takes rest of 5 minutes after travel of every 45 km, then find the time taken by P is how much more or less than time taken by a person who reached Manali 4th.
Find out the wrong number in the following number series.
5, 9, 25, 61, 125, 230
Find out the wrong number in the following number series.
80, 40, 20, 10, 2, 2.5
Find out the wrong number in the following number series.
50, 60, 80, 110, 180, 200
Find out the wrong number in the following number series.
1, 5, 40, 210, 1680, 15120
Find out the wrong number in the following number series.
100, 40, 200, 40, 400, 80
|
114 docs|51 tests
|
|
114 docs|51 tests
|


























