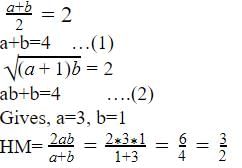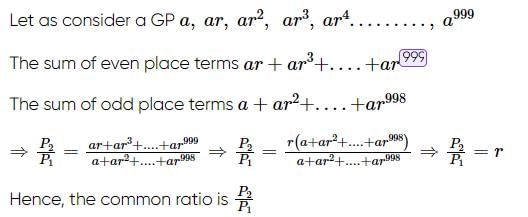Test: Progression (AP And GP)- 3 - CAT MCQ
15 Questions MCQ Test - Test: Progression (AP And GP)- 3
A group of friends have some money which was in an increasing GP. The total money with the first and the last friend was Rs 66 and the product of the money that the second friend had and that the last but one friend had was Rs 128. If the total money with all of them together was Rs 126, then how many friends were there?
The AM o f two given positive numbers is 2. I f the larger number is increased by 1, the GM of the numbers becomes equal to the AM of the given numbers. Then the HM of the given numbers is
A GP consists of 1000 terms. The sum of the terms occupying the odd places is Pj and the sum of the terms occupying the even places is P2. Find the common ratio of this GP.
If the roots of x3 - 12x2 + 39x - 28 = 0 are in an AP then their common difference is
If the nth term of AP is m and the nth term of the same AP is m, then (m + n)th term of AP is
If a, b and c are positive integers, then find the product of (a + b) (b + c) (c + a).
The mid-points of the adjacent sides of a square are joined. Again the mid-points of the adjacent sides of the newly formed figure are connected and this process is repeated again and again. Calculate the sum of the areas of all such figures given that the diagonal of outermost square is 6√2cm.
There are three numbers in arithmetic progression. If the two larger numbers are both increased by one, then the resulting numbers are prime. The product of these two primes and the smallest of the original numbers is 598. Find the sum of the three numbers.
In how many ways can we select three natural numbers out of the first 10 natural numbers so that they are in a geometric progression with the common ratio greater than 1?
If the sum of the first 2n terms of the AP 2, 5, 8... is equal to the sum of first n terms of the AP 57, 59, 6 . . . , then what is the value of nl
Given that (m +1l)th, (n + 1)th and (r +1l)th term of an AP are in GP and m , n , r are in HP, then find the ratio of the first term of the AP to its common difference in terms of n.
If a geometric mean of two non-negative numbers is equal to their harmonic mean, then which of the following is necessarily true?I. One of the numbers is zero.II. Both the numbers are equal.III. One of the numbers is one.
A series in which any term is the sum of the preceding two terms is called a Fibonacci series. The first two terms are given initially and together they determine the entire series. If the difference of the squares of the ninth and the eighth terms of a Fibonacci series is 715 then, what is the 12th term of that series?
The first term of an AP = the common ratio of a GP and the first term of the GP = common difference of the AP. If the sum of the first two terms of the GP is equal to the sum of the first 2 terms of the AP, then the ratio of the first term of the GP to the first term of an AP is