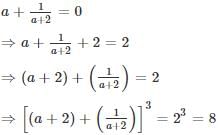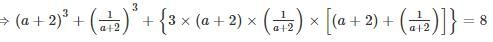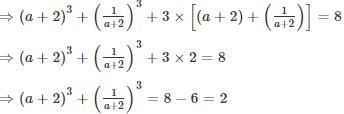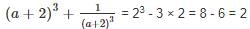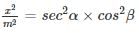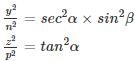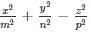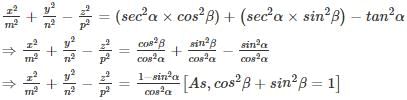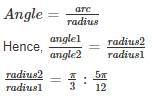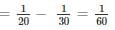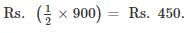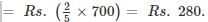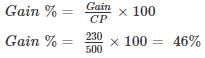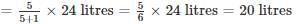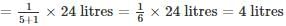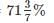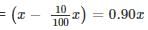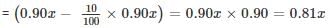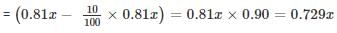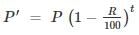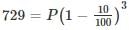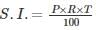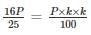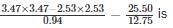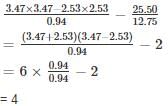Practice Test: Quantitative Aptitude - 10 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2024 - Practice Test: Quantitative Aptitude - 10
A cistern 5 m long and 8 m wide, contains water up to depth of 2 m 45 cm. Find the total area of wet surface.
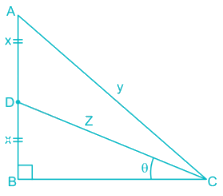
In a triangle ABC, ∠B = 90°, D is a point on line AB such that it divides AB into two equal parts. AB is denoted by 2x and AC by y, then find the value of sin θ where ∠DCB = θ°.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The area of a circle is proportional to the square of its radius. A small circle of radius 3 cm is drawn within a larger circle of radius 5 cm. find the ratio of the area of the annular zone to the area of the larger circle. (Area of the annular zone is the difference between the area of the larger circle and that of the smaller circle).
Directions: The production figure of a perfume manufactures are given in the form of percentage sub-divided bar diagram. Study the diagram and answer questions.
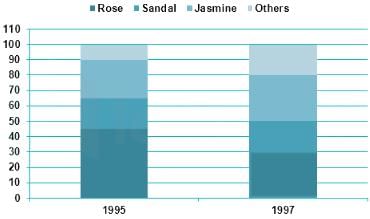
Q. What is the production of jasmine perfume in the year 1997? Given that during the year 1997 total perfumed production was 5000 units.
Directions: The production figure of a perfume manufactures are given in the form of percentage sub-divided bar diagram. Study the diagram and answer questions.
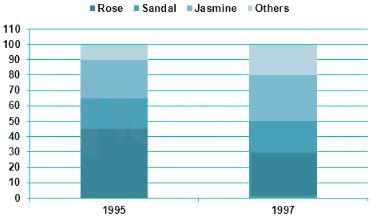
Q. What is the ratio of percentage production of rose perfume during 1995 to that during the year 1997?
Directions: The production figure of a perfume manufactures are given in the form of percentage sub-divided bar diagram. Study the diagram and answer questions.
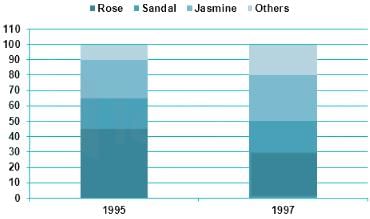
Q. What is the percentage increase of % production of sandal perfume during the year 1995 over that during 1997?
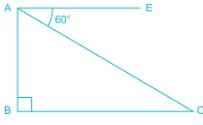
From a cliff 120 m above the shore of a sea, the angle of depression of a ship is 60°. Find the distance from the ship to a point on the shore directly below the observer.
x = m sec α cos β, y = n sec α sin β , z = p tan α , then the value of 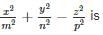
Sin232° + sin258° + cot258° is equal to
If the arcs of same length in two circles subtend angles of 60° and 75° at their centres, the ratio of their radii is
In Δ ABC, ∠A + ∠B = 65°, ∠B + ∠C = 140°, then find ∠B.
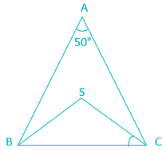
If S is the circumcentre of ΔABC and ∠A = 50°, then the value of ∠BCS is
A cistern is provided with two pipes A and B. A can fill it in 20 minutes and B can empty it in 30 minutes. If A and B be kept open alternately for one minute each, how soon will the cistern be filled?
A cyclist completes a certain journey in 5 hours. He covers half the distance at 16 km./hr. and the second half of the distance at 24 km./hr. The distance (in km) covered by the cyclist is?
Ram bought 1600 eggs at the rate of Rs. 3.75 per dozen. He sold 900 of them at 2 eggs for Rs. 1 and the remaining at 5 eggs for Rs. 2. Find his loss or gain per cent.
A 24 litres mixture contains milk and water in the ratio 5: 1. If 4 litres of water is mixed in the mixture, the percentage of milk in the new mixture is –
The average age of 11 players of a cricket team is increased by 2 months when two of them aged 18 years and 20 years are replaced by two new players. The average age of the new players is
The value of a machine depreciates every year at the rate of 10% on its value at the beginning of the year. If the current value of the machine is Rs.729, its worth 3 years ago was.
Simple interest on a certain sum is 16/25 of the sum. The rate per cent if the rate per cent and time (in years) are equal, is
The cost of a piece of diamond varies with the square of its weight. A diamond of Rs. 5,184 value is cut into 3 pieces whose weights are in the ratio 1 : 2 : 3. Find the loss involved in the cutting.
Convert 4.327327327.... into a rational expression.
|
237 docs|133 tests
|
|
237 docs|133 tests
|


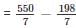
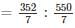
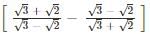 simplifies to
simplifies to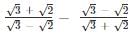
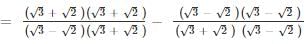
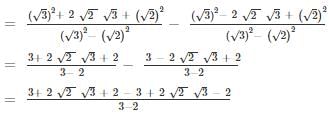
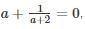 then the value of
then the value of