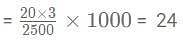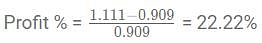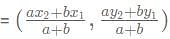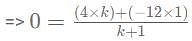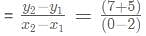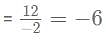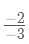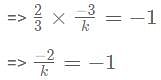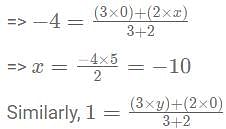Practice Test: Quantitative Aptitude - 12 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2024 - Practice Test: Quantitative Aptitude - 12
An employer reduces the number of employees in the ratio 8 : 5 and increases their wages in the ratio 7 : 9. As a result, the overall wages bill is
The ratio of ages of father and son is 7 : 2. Five years ago the product of their ages was 150. What is the age of the father?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The sum of the ages of husband and wife at present is 56. Ten years ago the product of their ages was 320. What is the age of the husband and the wife?
Ronald and Elan are working on an Assignment. Ronald takes 6 hours to type 32 pages on a computer, while Elan takes 5 hours to type 40 pages. How much time will they take working together on two different computers to type an assignment of 110 pages?
The ratio of present ages of Ramya and Saurabh is 8 : 7. After 10 years the ratio of their ages will be 12 : 11. What is Ramya's present age?
If 5x + 9y = 5 and 125x3 + 729y3 = 120 then the value of the product of x and y is
If m - 5n = 2, then the value of (m3 − 125n3 - 30 mn) is
Which of the following statement (s) is / are TRUE?
The 4th term of an arithmetic progression is 15, 15th term is -29, find the 10th term?
If 4x = 7√1024, then what is the value of x?
If the cost price of 15 articles is equal to the selling price of 12 articles, find gain %
A man bought an article listed at Rs. 1500 with a discount of 20% offered on the list price. What additional discount must be offered to man to bring the net price to Rs. 1,104?
A is 50% as efficient as B. C does half of the work done by A and B together. If C alone does the work in 20 days, then A, B and C together can do the work in
A man sold 20 apples for Rs. 1000 and gained 20%. How many apples did he buy for Rs. 1000?
A grain dealer cheats to the extent of 10% while buying as well as selling by using false weights. His total profit percentage is:
What is the equation of the line whose yintercept is 3/4 and making an angle of 45° with the positive x-axis?
In what ratio is the segment joining (-1, -12) and (3, 4) divided by the x-axis?
Find equation of the perpendicular bisector of segment joining the points (2, -5) and (0, 7)?
Find k, if the line 2x - 3y = 11 is perpendicular to the line 3x + ky = 4?
The point P(-4, 1) divides the segment joining the points (x, 0) and (0, y) in the ratio 3 : 2. Find x and y?
|
237 docs|133 tests
|
|
237 docs|133 tests
|



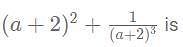
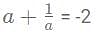

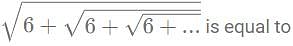
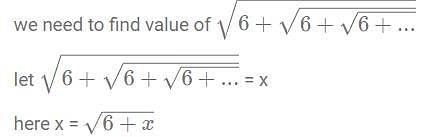
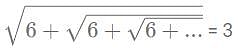

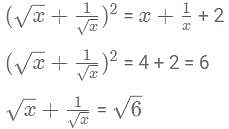
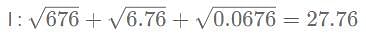
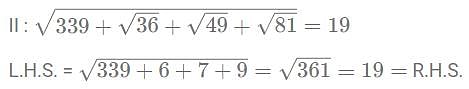
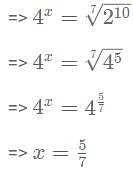
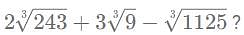
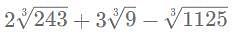
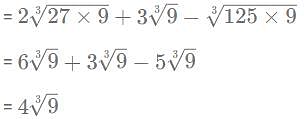
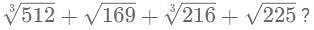
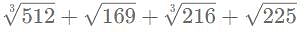
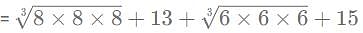
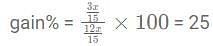
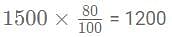

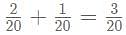 amount of work in a day.
amount of work in a day.