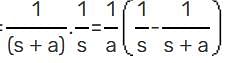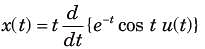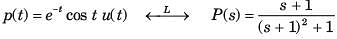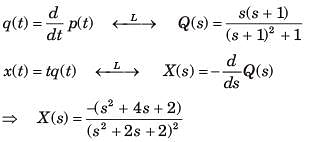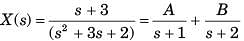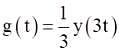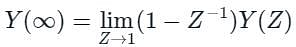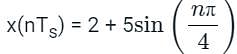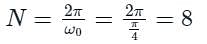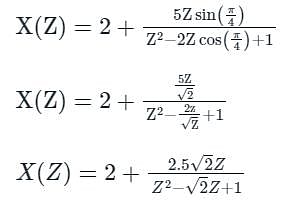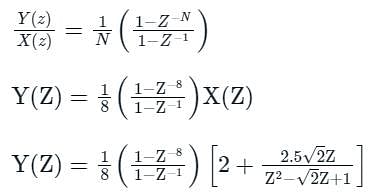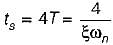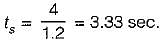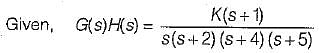Test: ESE Electrical - 6 - Electrical Engineering (EE) MCQ
30 Questions MCQ Test Engineering Services Examination (ESE) Mock Test Series 2024 - Test: ESE Electrical - 6
The Thevenin impedance across the terminals ab of the network shown in fig. P.1.4.8 is


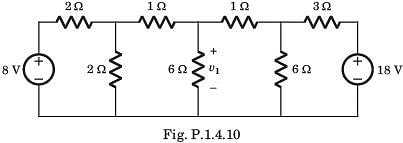
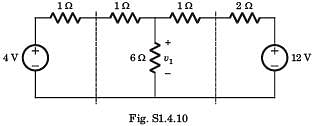
For In the the circuit shown in fig. P.1.4.9 a network and its Thevenin and Norton equivalent are given
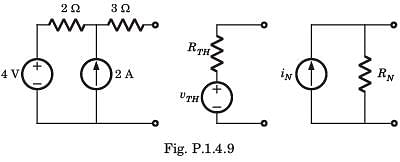
The value of the parameter are


The value of the parameter are

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the circuit shown in fig. a steady state has been established before switch closed. The i(t) for t > 0 is
The switch is closed after long time in the circuit of fig. The v(t) for t > 0 is
In the circuit of fig. i(0) = 1A and v(0) = 0. The current i(t) for t > 0 is

The T-parameters of a 2-port network are
If such two 2-port network are cascaded, the z –parameter for the cascaded network is
n a balanced three-phase system-delta load, if we assume the line voltage is VRY = V∠0⁰ as a reference phasor. Then the source voltage VBR is?
The three impedances Z1 = 20∠30⁰Ω, Z2 = 40∠60⁰Ω, Z3 = 10∠-90⁰Ω are delta-connected to a 400V, 3 – Ø system. Find the power in the B phase.
Find the magnetic force when a charge 3.5C with flux density of 4 units is having a velocity of 2m/s.
Find the electric field when the velocity of the field is 12m/s and the flux density is 8.75 units.
The unit impulse response of a linear time invariant system is the unit step function u(t) for t > 0, the response of the system to an excitation e-at u(t), a > 0 will be
What is the partial fraction expansion of the proper function X(z)= 1/(1-1.5z-1+0.5z-2 )?
What is the partial fraction expansion of X(z)= (1+z-1)/(1-z-1+0.5z-2 )?
Determine the time signal x(t) corresponding to given X (s) and choose correct option.
Q. 
The Fourier series coefficient of a periodic signal, x(t) is defined as

Which of the following statement is correct.
Find the value of A and B for signal, g(t) = Ay (Bt), such that y(t) = x (t) * h(t) and g(t) = x(3t) * h (3t) is
In the question, the FS coefficient of time-domain signal have been given. Determine the corresponding time domain signal and choose correct option.
An input signal x(t) = 2 + 5sin(100πt) is sampled with a sampling frequency of 400 Hz and applied to the system whose transfer function is represented by

where, N represents the number of samples per cycle. The output y[n] of the system under steady state is
If we split the N point data sequence into two N/2 point data sequences f1(n) and f2(n) corresponding to the even numbered and odd numbered samples of x(n) and F1(k) and F2(k) are the N/2 point DFTs of f1(k) and f2(k) respectively, then what is the N/2 point DFT X(k) of x(n)?
Which of the following defines the rectangular window function of length M-1?
How many memory locations are used for storage of the output point of a sequence of length M in direct form realization?
For the system shown in figure below, 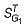 is equal to (where, T = closed loop transfer function)
is equal to (where, T = closed loop transfer function)

Use mason’s gain formula to find the transfer function of the following signal flow graph:
Consider the unity feedback system shown below:
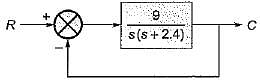
The settling time of the resulting second order system for 2% tolerance band will be
Consider the following characteristic equation of a system:
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?
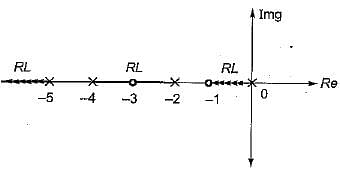
The open loop transfer function of a unity feedback control system is given by
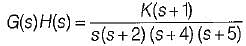
The breakaway point in its root locus will lie between


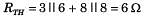



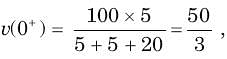

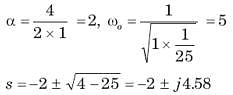

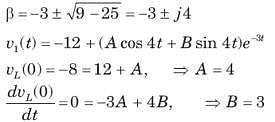
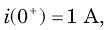


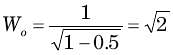


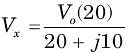
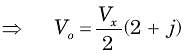
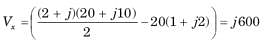
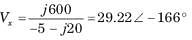
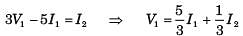 .......(i)
.......(i)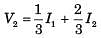 ........(ii)
........(ii)