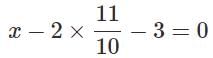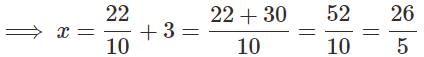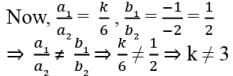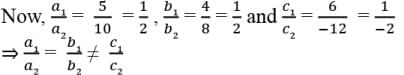Assertion & Reason Test: Pair of Linear Equations in Two Variables - Class 10 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 10 - Assertion & Reason Test: Pair of Linear Equations in Two Variables
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In a ΔABC, ∠C = 3∠B = 2(∠A + ∠B), then ∠A = 20°.
Reason (R): The angles of a triangle are x, y and 40°. The difference between the two angles x and y is 30°, then x = 85° and y = 55°.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The linear equations x - 2y - 3 = 0 and 3x + 4y - 20 = 0 = have exactly one solution.
Reason : The linear equations 2x + 3y - 0 = and 4x + 6y - 18 = 0 = have a unique solution.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations kx – y = 2 and 6x – 2y = 3 has a unique solution is 3.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The solution of the pair of linear equations x + y = 5 and 2x – 3y = 4 is x = 19/5 and y = 6/5.
Reason (R): The solution of the pair of linear equations 3x + 4y = 10 and 2x – 2y = 2 is x = 2 and y = 1.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : 3x - 4y = 7 and 6x - 8y = k have infinite number of solution if k = 14 .
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have a unique solution if a1/a2 ≠ b1/b2.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of q = ±2, if x = 3, y = 1 is the solution of the line 2x + y – q2 – 3 = 0.
Reason : The solution of the line will satisfy the equation of the line.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If 4 chairs and 3 tables cost ₹ 2100 and 5 chairs and 2 tables cost ₹ 1750, then the cost of 1 chair is ₹ 150.
Reason (R): Sum of the ages of a father and the son is 40 years. If father's age is 3 times that of his son, then the son's age is 12 years.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The lines 2x - 5y = 7 and 6x - 15y = 8 are parallel lines.
Reason : The system of linear equations a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions if a1/a2 = b1/b2 = c1/c2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : A pair of linear equations has no solution (s) if it is represented by intersecting lines graphically.
Reason: If the pair of lines are intersecting, then the pair has unique solution and is called consistent pair of equations.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the equation 3x – y + 8 = 0 and 6x – ky = –16 represent coincident lines, then the value of k = 2.
Reason (R): If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then the value of k is 15.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : If kx - y - 2 = 0 and 6x - 2y - 3 = 0 = are inconsistent, then k = 3
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are inconsistent of a1/a2 = b1/b2 ≠ c1/c2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The number of common solutions for the system of linear equations 5x + 4y + 6 = 0 and 10x + 8y = 12 is zero
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): For all real values of c, the pair of equations x – 2y = 8 and 5x – 10y = c have a unique solution.
Reason (R): Two lines are given to be parallel. The equation of one of the lines is 4x + 3y = 14, 12x + 9y = 5.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : Pair of linear equations : 9x + 3y + 12 = 0, 18x + 6y + 24 = 0 have infinitely many solutions.
Reason : Pair of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have infinitely many solutions, a1/a2 = b1/b2 = c1/c2
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : The value of k for which the system of linear equations 3x – 4y = 7 and 6x - 8y = k have infinite number of solution is 14.
Reason : The system of linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution if a1/a2 ≠ b1/b2
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|