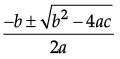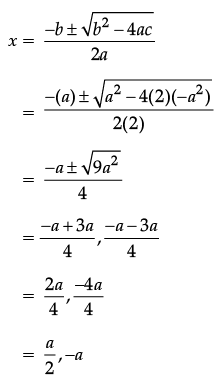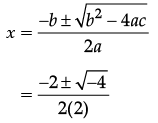Assertion & Reason Test: Quadratic Equation - Class 10 MCQ
10 Questions MCQ Test Mathematics (Maths) Class 10 - Assertion & Reason Test: Quadratic Equation
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The degree of quadratic equation is always 2. Hence, x2 – 1 = 0 is pure quadratic equation.
Reason (R): An equation of the form ax2 + c = 0 is known as pure quadratic equation.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The product of two successive positive integral multiples of 5 is 300, then the two numbers are 15 and 20.
Reason (R): The product of two consecutive integrals is a multiple of 2.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): In the expression: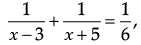 x can’t have values 3 and – 5
x can’t have values 3 and – 5
Reason (R): If discriminant D = b2 – 4ac > 0 then the roots of the quadratic equation ax2 + bx + c = 0 are real and unequal.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The equation 8x2 + 3kx + 2 = 0 has equal roots than the value of k is ± ![]()
Reason (R): The equation ax2 + bx + c = 0 has equal roots if D = b2 – 4ac = 0.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Values of x are ![]() a for a quadratic equation 2x2 + ax – a2 = 0.
a for a quadratic equation 2x2 + ax – a2 = 0.
Reason (R): For quadratic equation ax2 + ax + c = 0, 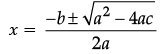
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Sum of ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Then the difference between their ages is 16.
Reason (R): For quadratic equation ax2 + bx + c = 0,
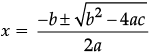
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The roots of the quadratic equation x2 + 2x + 2 = 0 are imaginary.
Reason (B): If discriminant D = b2 – 4ac < 0 then the roots of the quadratic equation ax2 + bx + c = 0 are imaginary.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If we solve the equation of the form 9(x+2) – 6.(3)(x+1) + 1 = 0, then x = – 2.
Reason (R): The equation of the form x2a + xb + b = 0 can’t be solved by quadratic formula.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The equation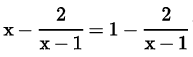 has no root.
has no root.
Reason (R): x - 1 ≠ 0, then only above equation is defined.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The equation x2 + 3x+1 = (x - 2)2 is a quadratic equation.
Reason : Any equation of the form ax2 + bx + c = 0 where a ≠ 0 , is called a quadratic equation.
|
126 videos|457 docs|75 tests
|