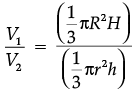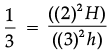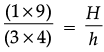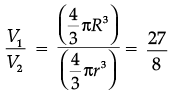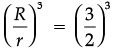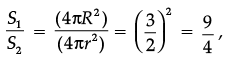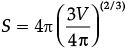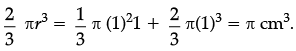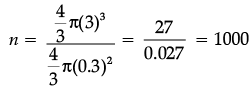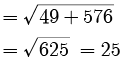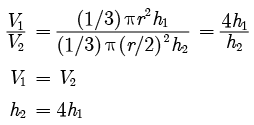Assertion & Reason Test: Surface Area & Volumes - Class 10 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 10 - Assertion & Reason Test: Surface Area & Volumes
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The radii of two cone are in the ratio 2 : 3 and their volumes in the ratio 1 : 3. Then ratio of their heights is 3 : 2.
Reason (R): Volume of Cone = 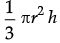
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the volume of two spheres are in the ratio 27 : 8. Then their surface area are in the ratio 3 : 2.
Reason (R): Volume of sphere = 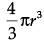 and its surface area = 4πr2.
and its surface area = 4πr2.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the height of the cone is 24 cm and diameter of the base is 14 cm, then the slant height of the cone is 15 cm.
Reason (R): If r be the radius of the cone and h be the height of the cone, then slant height = 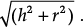
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The Volume and Surface Area of a sphere are related to each other by radius.
Reason (R): Relation between Surface Area S and Volume V is S3 = 36πV2.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): A solid is in the form of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. The volume of the solid is π cm3.
Reason (R): Volume of cone = ![]() and volume of hemi-sphere =
and volume of hemi-sphere = ![]()
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): There are 1000 balls of diameter 0.6 cm which can be formed by melting a solid sphere of radius 3 cm.
Reason (R):Number of spherical balls = (Volume of Bigger solid sphere)/(Volume of 1 spherical ball)
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): A solid iron is in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm is melted to form a solid sphere. Then the radius of sphere will be 21 cm.
Reason (R): Volume of cylinder = πr2h, r is the radius of the cylinder and h is the height of the cylinder.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): A manufacturer involved children in colouring playing top (Lattu) which is shaped like a cone surmounted by a hemisphere. The entire top is 5 cm in height and the diameter of the top is 3.5 cm. The area to be painted if 100 playing tops are given to him then will be 3955 cm2.
Reason (R): Slant height = ![]()
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Total surface area of the cylinder having radius of the base 14 cm and height 30 cm is 3872 cm2 .
Reason : If r be the radius and h be the height of the cylinder, then total surface area = (2prh +2pr2).
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If the height of a cone is 24 cm and diameter of the base is 14 cm, then the slant height of the cone is 15 cm.
Reason : If r be the radius and h the slant height of the cone, then slant height = ![]()
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If the radius of a cone is halved and volume is not changed, then height remains same.
Reason : If the radius of a cone is halved and volume is not changed then height must become four times of the original height.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If a ball is in the shape of a sphere has a surface area of 221.76cm2 , then its diameter is 8.4 cm.
Reason : If the radius of the sphere be r , then surface area, S = 4p r2 , i.e. ![]()
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : No. of spherical balls that can be made out of a solid cube of lead whose edge is 44 cm, each ball being 4 cm. in diameter, is 2541
Reason : Number of balls ![]()
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The slant height of the frustum of a cone is 5 cm and the difference between the radii of its two circular ends is 4 cm. Than the height of the frustum is 3 cm.
Reason : Slant height of the frustum of the cone is given by ![]()
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Two identical solid cube of side 5 cm are joined end to end. Then total surface area of the resulting cuboid is 300 cm2 .
Reason : Total surface area of a cuboid is 2(lb + bh + lh)
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|