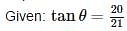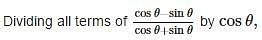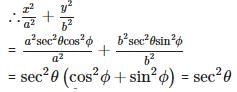Important Question (1 Mark): Introduction to Trigonometry - Class 10 MCQ
25 Questions MCQ Test Online MCQ Tests for Class 10 - Important Question (1 Mark): Introduction to Trigonometry
If sin θ = 5/13 then cos θ =
Which of the following is true:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If √3tanθ = 3sinθ, then the value of sin2θ−cos2θ is
If sec A + tan A = m and sec A – tan A = n, then the value of mn is
If sin θ − cos θ = 0, vthen the value of θ is
If tan θ = √3, the sec θ =
Given that sin A=1/2 and cos B=1/√2 then the value of (A + B) is:
If cot θ = 7/8, then the value of (1 + sin θ)(1 - sin θ) / (1 + cos θ)(1 - cos θ)
Given that sinθ = a/b then cos θ is equal to
If (α + β) = 90°, then the value of 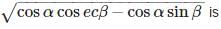
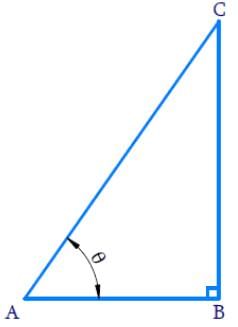
In right triangle ABC, right angled at C, if tan A = 1, then the value of 2 sin A cos A is
The value of sin60∘cos30∘ + sin30∘cos60∘ is
If sin θ − cos θ = 0, then the value of sin4θ + cos4θ is
If x = a cos θ and y = b sin θ, then the value of b2x2 + a2y2 is
The value of 2 tan245∘+ cos230∘ − sin260∘ is
The value of tan 1∘ tan 2∘ tan 3∘………… tan 89∘ is
(sec2θ - 1) (1 - cosec2θ) =
If x = a sec θ cos φ, y = b sec θ sin φ and z = c tan θ, then the value of 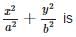
|
461 tests
|



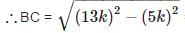
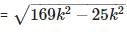
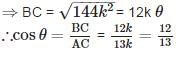
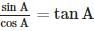 is correct.
is correct.