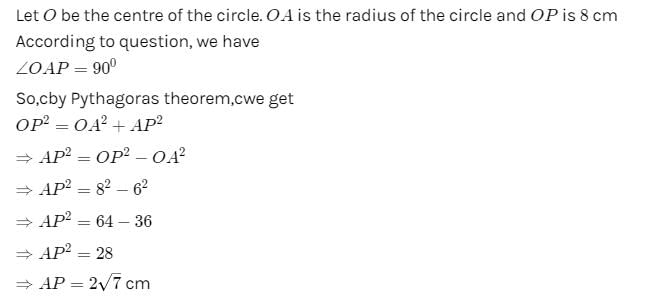Class 10 Exam > Class 10 Tests > Mathematics (Maths) Class 10 > Important Questions: Circles - Class 10 MCQ
Important Questions: Circles - Class 10 MCQ
Test Description
10 Questions MCQ Test Mathematics (Maths) Class 10 - Important Questions: Circles
Important Questions: Circles for Class 10 2024 is part of Mathematics (Maths) Class 10 preparation. The Important Questions: Circles questions and answers have been
prepared according to the Class 10 exam syllabus.The Important Questions: Circles MCQs are made for Class 10 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Important Questions: Circles below.
Solutions of Important Questions: Circles questions in English are available as part of our Mathematics (Maths) Class 10 for Class 10 & Important Questions: Circles solutions in
Hindi for Mathematics (Maths) Class 10 course. Download more important topics, notes, lectures and mock
test series for Class 10 Exam by signing up for free. Attempt Important Questions: Circles | 10 questions in 10 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study Mathematics (Maths) Class 10 for Class 10 Exam | Download free PDF with solutions
Important Questions: Circles - Question 1
If angle between two radii of a circle is 130°, the angle between the tangents at the ends of the radii is
Important Questions: Circles - Question 2
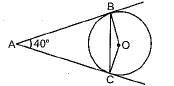
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°, then ∠BOC is equal to
Detailed Solution for Important Questions: Circles - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Important Questions: Circles - Question 3
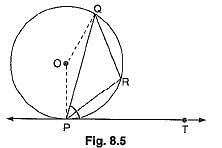
In Fig. 8.5, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT = 60°. Then ∠PRQ is equal to
Detailed Solution for Important Questions: Circles - Question 3
Important Questions: Circles - Question 4
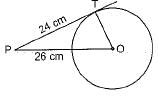
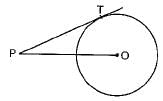
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is
Detailed Solution for Important Questions: Circles - Question 4
Important Questions: Circles - Question 5
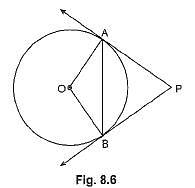
In Fig. 8.6, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠PAB is equal to
Detailed Solution for Important Questions: Circles - Question 5
Important Questions: Circles - Question 6
A line through point of contact and passing through centre of circle is known as
Important Questions: Circles - Question 7
The length of the taragent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
Detailed Solution for Important Questions: Circles - Question 7
Important Questions: Circles - Question 8
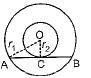
C (O, r1) and C (O, r2) are two concentric circles with r1 > r2. AB is a chord of C (O, r1) touching C (O, r2) at C then
Detailed Solution for Important Questions: Circles - Question 8
Important Questions: Circles - Question 10
Two parallel lines touch the circle at points A and B respectively, If area of the circle is 25πcm2, then AB is equal to
Detailed Solution for Important Questions: Circles - Question 10
|
124 videos|457 docs|77 tests
|
Information about Important Questions: Circles Page
In this test you can find the Exam questions for Important Questions: Circles solved & explained in the simplest way possible.
Besides giving Questions and answers for Important Questions: Circles, EduRev gives you an ample number of Online tests for practice
|
124 videos|457 docs|77 tests
|
Download as PDF
Top Courses for Class 10
Important Questions: Circles
Find all the important questions for Important Questions: Circles at EduRev.Get fully prepared for Important Questions: Circles with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Important Questions: Circles syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Important Questions: Circles resources.
Important Questions: Circles MCQs with Answers
Prepare for the Important Questions: Circles within the Class 10 exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Important Questions: Circles Mathematics (Maths) Class 10
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Important Questions: Circles with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup