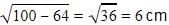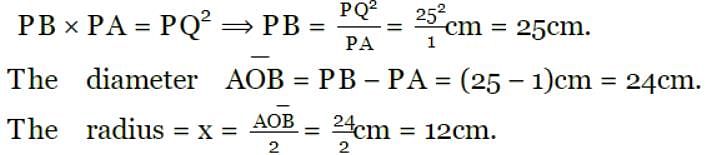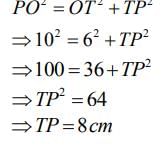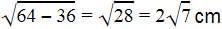Practice Test: Circles - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - Practice Test: Circles
A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to
A point P is 25 cm from the centre of a circle. The radius of the circle is 7 cm and length of the tangent drawn from P to the circle is x cm. The value of x =
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
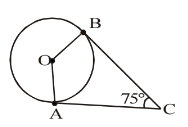
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =
In fig, O is the centre of the circle. PQ is tangent to the circle and secant PAB passes through the centre O. If PQ = 5 cm and PA = 1 cm, then the radius of the circle is
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
The length of the tangent from a point A at a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80° then ∠POA is equal to
If TP and TQ are two tangents to a circle with centre O so that ∠POQ = 110°, then, ∠PTQ is equal to
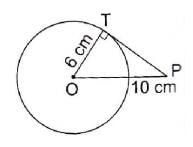
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is
Two circle touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB =
ABC is a right angled triangle, right angled at B such that BC = 6 cm and AB = 8 cm. A circle with centre O is inscribed in ΔABC. The radius of the circle is
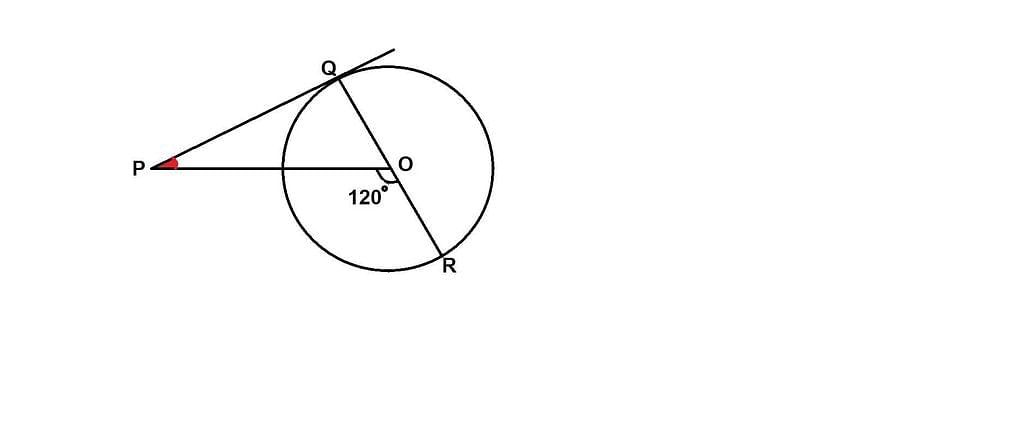
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°, then ∠OPQ is
If four sides of a quadrilateral ABCD are tangential to a circle, then
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
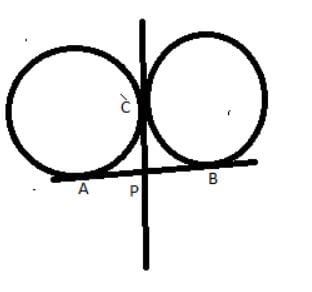
AB and CD are two common tangents to circles which touch each other at C. If D lies on AB such that CD = 4 cm, then AB is equal to
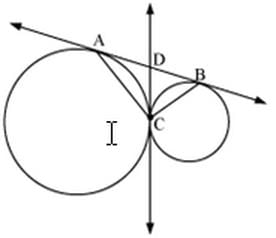
In the adjoining figure, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then,
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD :
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ = 15 cm, PR = 25 cm, find PN:
In the given figure, there are two circles with the centres O and O' touching each other internally at P. Tangents TQ and TP are drawn to the larger circle and tangents TP and TR are drawn to the smaller circle. Find TQ : TR
In the given figure, PAQ is the tangent. BC is the diameter of the circle. m ∠BAQ = 60°, find m ∠ABC :
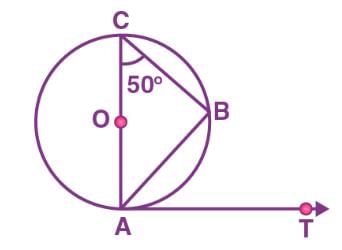
AB is a chord of the circle and AOC is its diameter such that angle ACB = 50°. If AT is the tangent to the circle at the point A, then BAT is equal to
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|