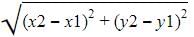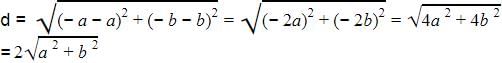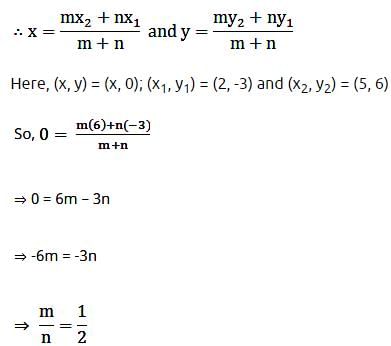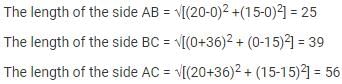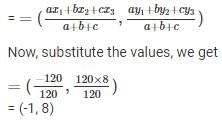Practice Test: Coordinate Geometry - Class 10 MCQ

The distance between the points (a cos 20° + b sin 20°, 0) and (0, a sin 20° – b cos 20°) is :

Mid-point of the line-segment joining the points (– 5, 4) and (9, – 8) is :

The co-ordinates of the points which divides the join of (– 2, – 2) and (– 5, 7) in the ratio 2 : 1 is :

The co-ordinates of the point on x-axis which is equidistant from the points (5, 4) and (– 2, 3) are :

The co-ordinates of the point on y-axis which is equidistant from the points (3, 1) and (1, 5) are:

The coordinates of the centre of a circle are (– 6, 1.5). If the ends of a diameter are (– 3, y) and (x, – 2) then:

The points (– 2, 2), (8, – 2) and (– 4, – 3) are the vertices of a :

The points (1, 7), (4, 2), (– 1, 1) and (– 4, 4) are the vertices of a :

The line segment joining (2, – 3) and (5, 6) is divided by x-axis in the ratio:

The line segment joining the points (3, 5) and (– 4, 2) is divided by y-axis in the ratio:

If (3, 2), (4, k) and (5, 3) are collinear then k is equal to :

If the points (p, 0), (0, q) and (1, 1) are collinear then 1/p+1/q is equal to :

Two vertices of a triangle are (–2, – 3) and (4, –1) and centroid is at the origin. The coordinates of the third vertex of the triangle are :

A (5, 1), B(1, 5) and C (–3, –1) are the vertices of ?ABC. The length of its median AD is :

Three consecutive vertices of a parallelogram are (1, –2), (3, 6) and (5, 10). The coordinates of the fourth vertex are :

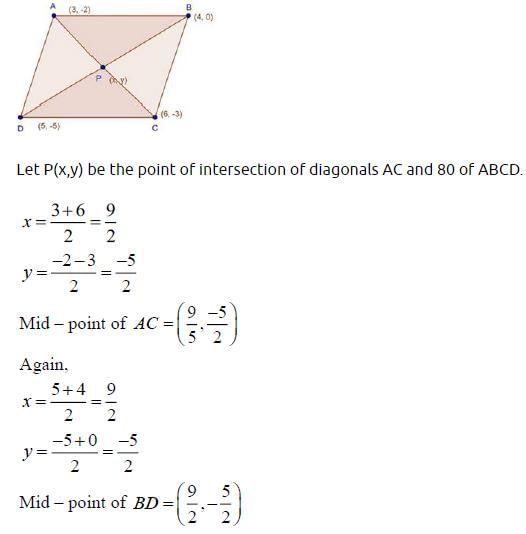
The vertices of a parallelogram are (3, –2), (4, 0), (6, –3) and (5, –5). The diagonals intersect at the point M. The coordinates of the point M are :

If two vertices of a parallelogram are (3, 2) and (–1, 0) and the diagonals intersect at (2, –5), then the other two vertices are :

The circumcentre of the triangle formed by the lines xy + 2x + 2y + 4 = 0 and x + y + 2 = 0 is :

The vertices of a triangle are (a, b – c), (b, c – a) and (c, a – b), then it's centroid lies on :

The points (1, 2), (3, 8) and (x, 20) are collinear if x =

For the triangle whose sides are along the lines x = 0, y = 0 and x/6+y/8 = 1, the incentre is :

For the triangle whose sides are along the lines y = 15, 3x – 4y = 0, 5x + 12y = 0, the incentre is :