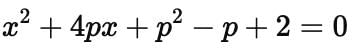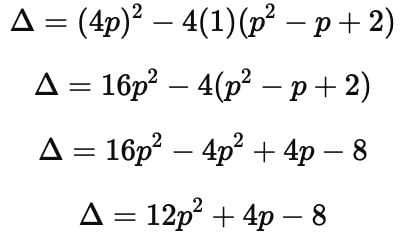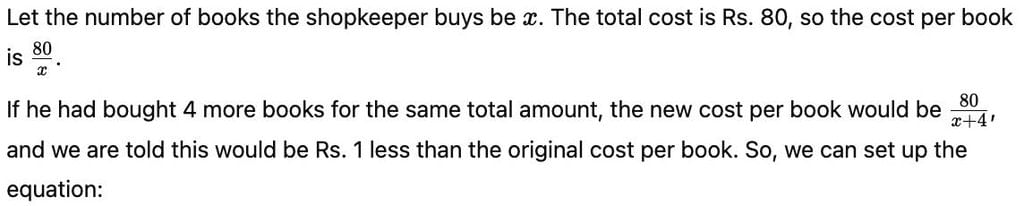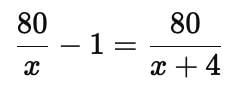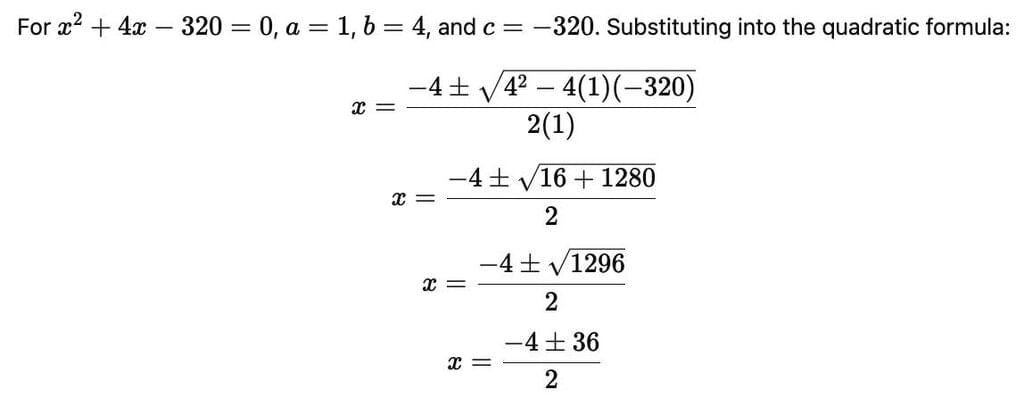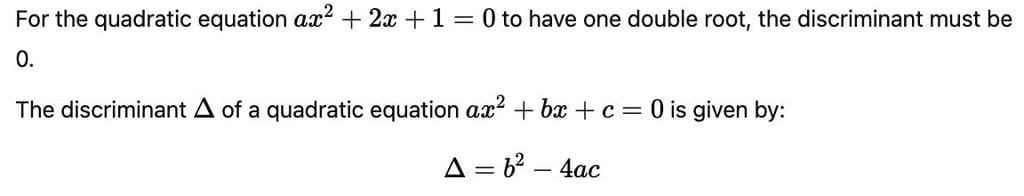Practice Test: Quadratic Equations - Class 10 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 10 - Practice Test: Quadratic Equations
Which of the following quadratic expression can be expressed as a product of real linear factors?
One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son’s age. Their present ages are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Discriminant of the equation: ( – 3x2 + 2x – 8 = 0 ) is
The nature of the roots of the equation x2 – 5x + 7 = 0 is –
Determine the value of k for which the quadratic equation 4x2 – 3kx + 1 = 0 has equal roots :
Find the value of p for which the quadratic equation x2 + p(4x + p – 1) + 2 = 0 has equal roots :
A two digit number is such that the product of it's digits is 12. When 9 is added to the number, the digits interchange their places, find the number :
The equation 12x² + 4kx + 3 = 0 has real and equal roots, if
The roots of the equation (b – c) x² + (c – a) x + (a – b) = 0 are equal, then
The sum of the squares of two consecutive positive odd numbers is 290. Find the sum of the numbers :
A shopkeeper buys a number of books for Rs. 80. If he had bought 4 more for the same amount, each book would have cost Re. 1 less. How many books did he buy?
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm2. Find the sides of the square.
Equation ax2 + 2x + 1 has one double root if :
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|


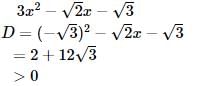

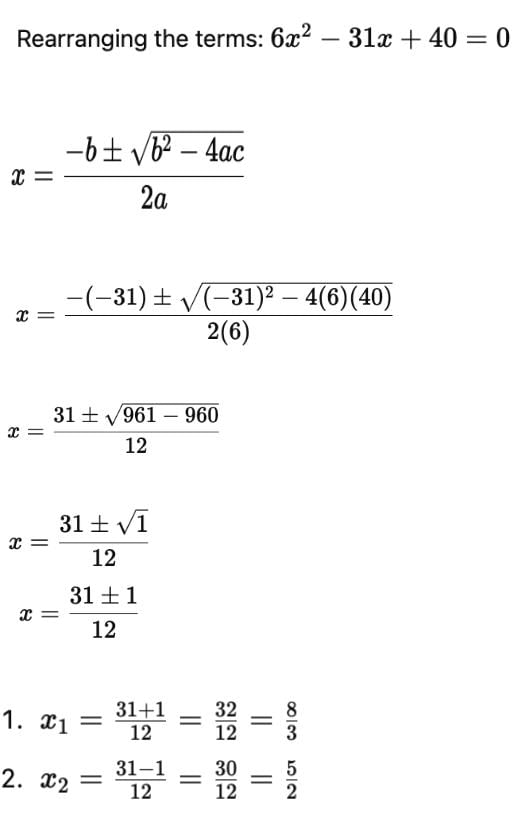

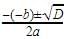 , Since we do not have any real number which is a root of a negative number, the roots are not real.
, Since we do not have any real number which is a root of a negative number, the roots are not real.