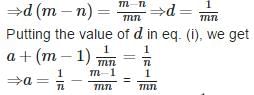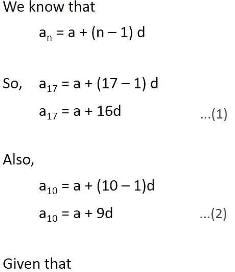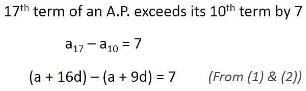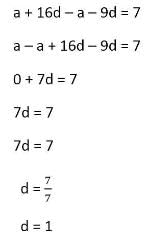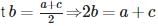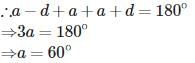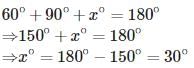RD Sharma Test: Arithmetic Progressions - Class 10 MCQ
25 Questions MCQ Test Online MCQ Tests for Class 10 - RD Sharma Test: Arithmetic Progressions
Progressions with equal common difference are known as
The first term of an A.P., if its Sn = n2+2n is
If the second term of an AP is 13 and its fifth term is 25, then its 7th term is
In an A.P., if am = 1/n and an = 1/m, then amn =
The first term of an AP is 5, the last term is 45 and the sum is 400. The number of terms is
The value of ‘k’ for which the numbers x, 2x + k, 3x + 6 are in A.P. is
If the common difference of an A.P. is 5, then the value of a20 − a13 is
Two APs have the same common difference. The difference between their 100th terms is 100, then the difference between their 1000th terms is
The common difference of the A.P whose Sn = 3n2+ 2n is
The sum of (a + b), (a – b), (a – 3b), …….. to 22nd term is
The next term of the A.P. √18 , √32 and √50 is
If 9 times the 9th term of an A.P. is equal to 11 times the 11th term , then its 20th term is
The 17th term of an AP exceeds its 10th term by 7, then the common difference is
The sum of three terms of an A.P. is 72, then its middle term is
The sum of odd numbers between 0 and 50 is
If a, b and c are in A.P., then the relation between them is given by
The 7th term from the end of the A.P. – 11, – 8, – 5, ……., 49 is
The number of three digit numbers divisible by 7 is
The first and last terms of an A.P. are 1 and 11. If their sum is 36, then the number of terms will be
If 1 + 4 + 7 + ……. + k = 287, then the value of ‘k’ is
If the angles of a right angled triangle are in A.P. then the angles of that triangle will be
The 10th term of an A.P. 2, 7, 12, …….. is
If a1 = 4 and an = 4an−1+3, n >1, then the value of a4 is
The number of terms of the A.P. 5, 8, 11, 14, ……. to be taken so that the sum is 258 is
A sum of Rs.700 is to be used to award 7 prizes. If each prize is Rs.20 less than its preceding prize, then the value of the first prize is
|
461 tests
|