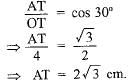RS Aggarwal Test: Circles - Class 10 MCQ
10 Questions MCQ Test Online MCQ Tests for Class 10 - RS Aggarwal Test: Circles
In Fig. 8.4, the pair of tangents AP and AQ drawn from an external point A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. Then radius of the circle is


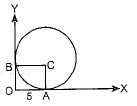
A circle touches x-axis at A and y-axis at B. If O is origin and OA = 5 units, then diameter of the circle is
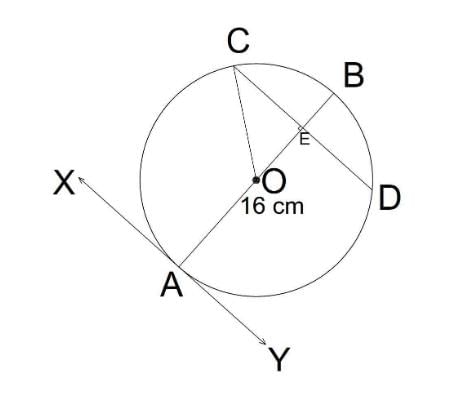
At point A on a diameter AB of a circle of radius 10 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY at a distance 16 cm from A is
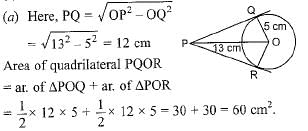
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
Two circles touch each other externally at C and AB is common tangent of circles, then ∠ACB is
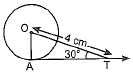
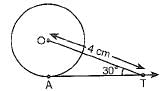
In figure AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to
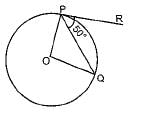
In Fig. 8.8, if PA anti PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to

In figure if O is centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to
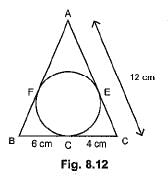
If ΔABC is circumscribing a circle in the Fig. 8.12. The length of AB is
From a point X, the length of the tangent to a circle is 20 cm and the distance of X from the centre is 25 cm. The radius of the circle is
|
461 tests
|