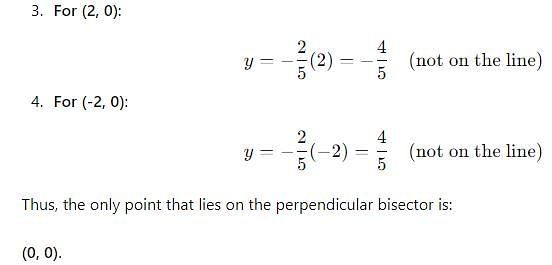RS Aggarwal Test: Coordinate Geometry - Class 10 MCQ
10 Questions MCQ Test Mathematics (Maths) Class 10 - RS Aggarwal Test: Coordinate Geometry
The mid-point of the line segment joining the points A (-2, 8) and B (-6, -4) is
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The distance of the point P (2, 3) from the x-axis is
If  is the mid-point of the line segment joining the points Q (-6, 5) and E (-2, 3), then the value of a is
is the mid-point of the line segment joining the points Q (-6, 5) and E (-2, 3), then the value of a is
The distance of the point P (-6, 8) from the origin is
The points (k + 1, 1), (2k + 1, 3) and (2k + 2, 2k) are collinear if
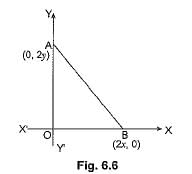
The coordinates of the point which is equidistant from the three vertices of the triangle shown in the given Fig. 6.6 are
The area of a triangle with vertices A (3, 0), B (7, 0) and C (8, 4) is
The points which lies on the perpendicular bisector of the line segment joining the points A (-2, -5), B (2, 5) is
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|