Test: Equations Reducible to Quadratic Form - Class 10 MCQ
10 Questions MCQ Test Online MCQ Tests for Class 10 - Test: Equations Reducible to Quadratic Form
Ruhi’s mother is 26 years older than her. The product of their ages (in years) 3 years from now will be 360. Form a Quadratic equation so as to find Ruhi’s age
Divide 16 into two parts such that twice the square of the larger part exceeds the square of the smaller part by 164.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If ax2 + bx + c, a ≠ 0 is factorizable into product of two linear factors, then roots of ax2 + bx + c = 0 can be found by equating each factor to
Reduction of a rupee in the price of onion makes the possibility of buying one more kg of onion for Rs.56. Find the original price of the onion per kg?
What are the two consecutive even integers whose squares have sum 340?
The length of the plot in meters is 1 more than twice its breadth and the area of a rectangle plot is 528m2. Which of the following quadratic equations represents the given situation:
Find the two consecutive odd positive integers, sum of whose square is 290
If the length of the rectangle is one more than the twice its width, and the area of the rectangle is 300 square meter. What is the measure of the width of the rectangle?
The sum of areas of two squares is 468m2. If the difference of their perimeters is 24m, then the sides of the two squares are:
If b2 - 4ac = 0 then The roots of the Quadratic equation ax2 + bx + c = 0 are given by :
|
461 tests
|



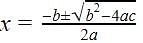

 So there are repeated roots
So there are repeated roots















