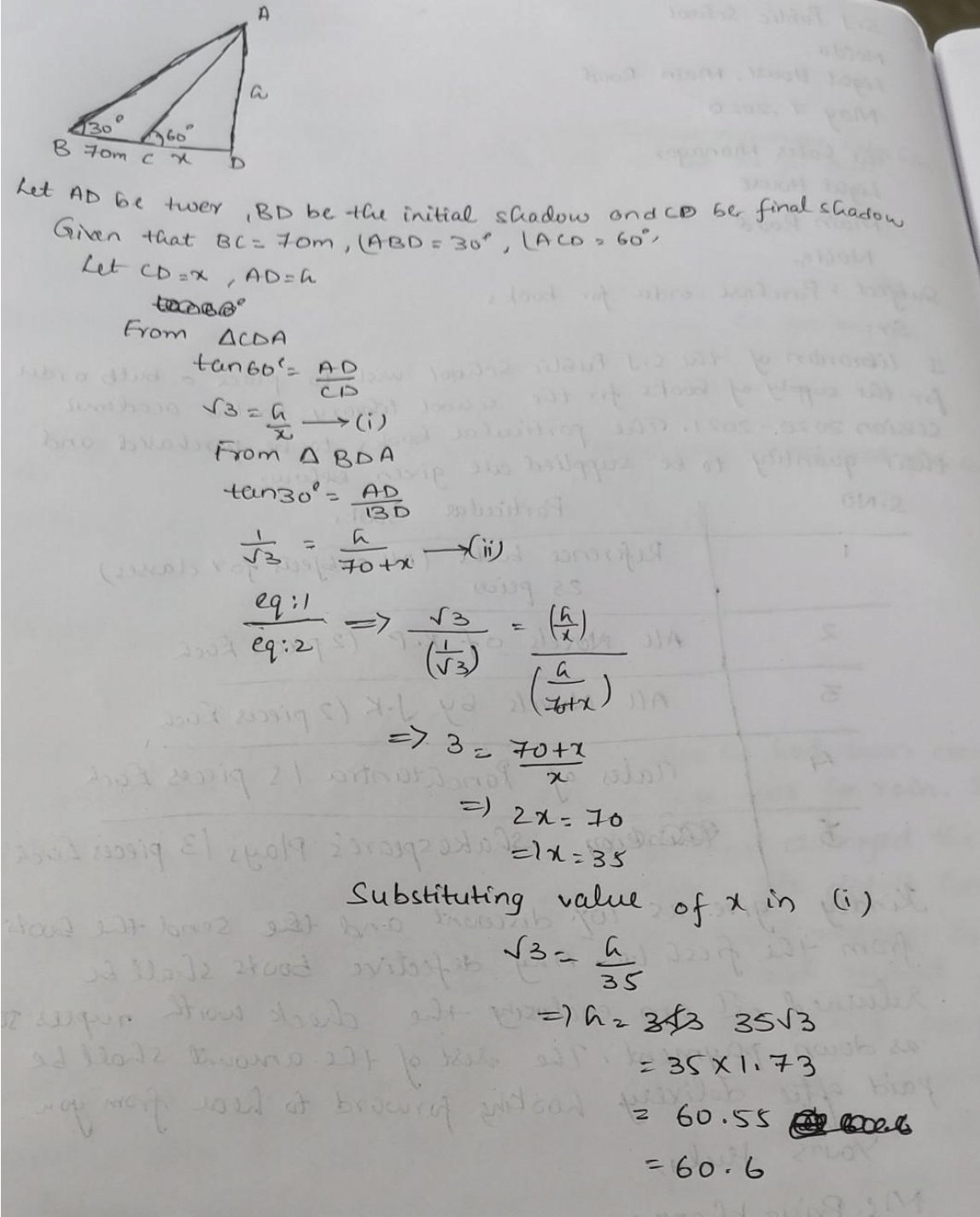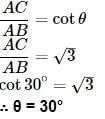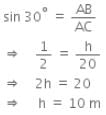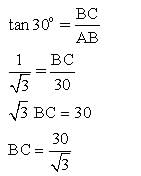Test: Introduction to Heights & Distances - Class 10 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 10 - Test: Introduction to Heights & Distances
When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?
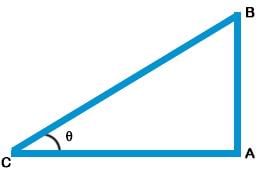
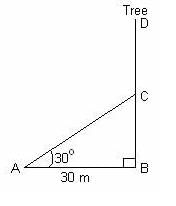
The fig., shows the observation of point C from point A. The angle of depression from A is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level is called:
A tower stands vertically on the ground from a point on the ground which is 25 m away from the foot of tower if the height of tower is 25√3 metres find the angle of elevation.
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is
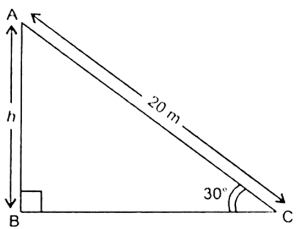
Let AC be the rope whose length is 20 m, and AB be the vertical pole of height h m and the angle of elevation of A at point C on the ground is 30°.
A 20 m long ladder touches the wall at a height of 10 m. The angle which the ladder makes with the horizontal is
The ratio of the length of a rod and its shadow is 1:1/√3. what is the angle of elevation of the source of light
If sun’s elevation is 60° then a pole of height 6 m will cast a shadow of length
The angle of elevation from a point 30 metre from the base of tree as level ground to the top of the tree is 60°. The height of the tree is :
Tree is broken by the wind the top struck the ground at 30degree at a distance of 30m. away from the root. Find the height of the tree.
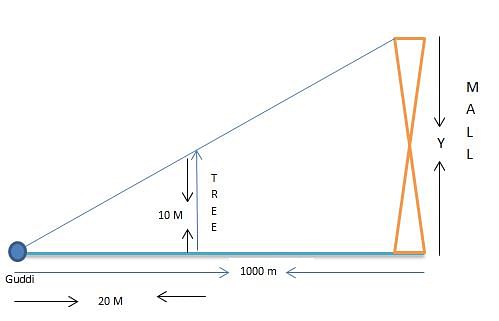
Guddi was standing on a road near a mall. She was 1000m away from the mall and able to see the top of the mall from the road in such a way that top of the tree, which is in between her and the mall, was exactly in line of sight with the top of the mall. The tree height is 10m and it is 20m away from Guddi. How tall is the mall?
A tower stands vertically on the ground. From a point C on the ground, which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45 degrees. The height of the tower is
The angle of elevation from a point 30 feet from the base of a pole, of height h, as level ground to the top of the pole is 45o. Which equation can be used to find the height of the pole.
A tree casts a shadow 4 m long on the ground, when the angle of elevation of the sun is 45°. The height of the tree is:
The angle of elevation of the sun when the length of the shadow of the tree is √3 times the height of the tree is
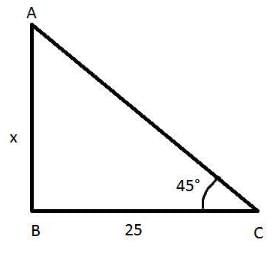
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45o. Then the height (in meters) of the tower is
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|