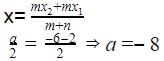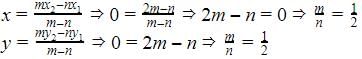Test: Section Formula - Class 10 MCQ
15 Questions MCQ Test Online MCQ Tests for Class 10 - Test: Section Formula
The coordinates of a point A, where AB is diameter of a circle whose centre is (2,-3) and B is (1, 4), are:
If 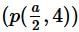 is the mid-point of the line-segment joining the points A (-6, 5) and B (-2,3) then the value of a is
is the mid-point of the line-segment joining the points A (-6, 5) and B (-2,3) then the value of a is
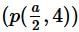 is the mid-point of the line-segment joining the points A (-6, 5) and B (-2,3) then the value of a is
is the mid-point of the line-segment joining the points A (-6, 5) and B (-2,3) then the value of a isThe ratio in which the point P(-3,y) divides the line segment joining the points A(-5,-4) and B(-2,3) is
The coordinates of the point which divide the line segment joining P (-2, 2) and Q (2, 8) into two equal parts are:
The mid-point of the line segment joining P(-2,8) and Q(-6,-4) is
Determine the ratio in which the line 2x+y-4 = 0 divides the line segment joining the points A (2,-2) and B (3, 7)
The mid point of the line segment joining A(2a,4) and B(-2,3b) is M (1,2a + 1). The values of a and b are
The ratio in which the x-axis divides the segment joining A(3,6) and B(12,-3) is
The ratio in which the line 2x+y-4 = 0 divides the line segment joining A(2,-2) and B(3,7) is
If A (1,2) , B (4,y), c (x,6) and D (3,5) are the vertices of a parallelogram taken in order then the values of x and y are:
The ratio in which the line segment joining A(3,4) and B(-2,1) is divided by the y-axis is
The line segment joining A(-2,9), and B(6,3) is a diameter of a circle with centre C. The co-ordinates of C are
The coordinates of the point which divides the line segment joining points A(5,-2) and B(9,6) in the ratio 3:1 are
The ratio in which (4,5) divides the line segment joining the points (2,3) and (7,8) is
Origin divides the join of points (1,1) and (2,2) externally in the ratio
|
461 tests
|