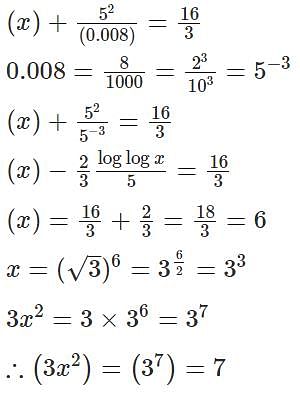CAT 2023 Slot 2: Past Year Question Paper - CAT MCQ
30 Questions MCQ Test CAT Mock Test Series 2024 - CAT 2023 Slot 2: Past Year Question Paper
The central idea of the passage would be undermined if:
The act of "thrifting", as described in the passage, can be considered ironic because it:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Based on the passage, we can infer that the opposite of fast fashion, ‘slow fashion’, would most likely refer to clothes that:
According to the author, companies like ThredUP have not caught on in the UK for all of the following reasons EXCEPT that:
The author of the passage faults Deneen's conclusions for all of the following reasons, EXCEPT:
The author of the passage is likely to disagree with all of the following statements, EXCEPT:
All of the following statements are evidence of the decline of liberalism today, EXCEPT:
The author of the passage refers to "the Davos elite" to illustrate his views on:
All of the following, if true, can weaken the passage's claim that facts do not speak for themselves, EXCEPT:
If the author of the passage were to write a book on the Battle of Hastings along the lines of his/her own reasoning, the focus of the historical account would be on:
According to this passage, which one of the following statements best describes the significance of archaeology for historians?
All of the following describe the "common-sense view" of history, EXCEPT:
Based on information provided in the passage, all of the following are true, EXCEPT:
The author sees the rise of Netflix in Europe as:
Which one of the following research findings would weaken the author's conclusion in the final paragraph?
Based only on information provided in the passage, which one of the following hypothetical Netflix shows would be most successful with audiences across the EU?
There is a sentence that is missing in the paragraph below. Look at the paragraph and decide where (option 1, 2, 3, or 4) the following sentence would best fit.
Sentence: And probably much earlier, moving the documentation for kissing back 1,000 years compared to what was acknowledged in the scientific community.
Paragraph: Research has hypothesised that the earliest evidence of human lip kissing originated in a very specific geographical location in South Asia 3,500 years ago.___(1)___. From there it may have spread to other regions, simultaneously accelerating the spread of the herpes simplex virus 1. According to Dr Troels Pank Arbøll and Dr Sophie Lund Rasmussen, who in a new article in the journal Science draw on a range of written sources from the earliest Mesopotamian societies, kissing was already a well-established practice 4,500 years ago in the Middle East.___(2)___. In ancient Mesopotamia, people wrote in cuneiform script on clay tablets.___(3)___. Many thousands of these clay tablets have survived to this day, and they contain clear examples that kissing was considered a part of romantic intimacy in ancient times.___(4)___. "Kissing could also have been part of friendships and family members' relations," says Dr Troels Pank Arbøll, an expert on the history of medicine in Mesopotamia.
There is a sentence that is missing in the paragraph below. Look at the paragraph and decide where (option 1, 2, 3, or 4) the following sentence would best fit.
Sentence: Dualism was long held as the defining feature of developing countries in contrast to developed countries, where frontier technologies and high productivity were assumed to prevail.
Paragraph: ___(1)___. At the core of development economics lies the idea of 'productive dualism': that poor countries' economies are split between a narrow 'modern' sector that uses advanced technologies and a larger 'traditional' sector characterized by very low productivity.___(2)___. While this distinction between developing and advanced economies may have made some sense in the 1950s and 1960s, it no longer appears to be very relevant. A combination of forces have produced a widening gap between the winners and those left behind.___(3)___. Convergence between poor and rich parts of the economy was arrested and regional disparities widened.___(4)___. As a result, policymakers in advanced economies are now grappling with the same questions that have long preoccupied developing economies: mainly how to close the gap with the more advanced parts of the economy.
Five jumbled up sentences (labelled 1, 2, 3, 4 and 5), related to a topic, are given below. Four of them can be put together to form a coherent paragraph. Identify the odd sentence
1. Self-care particularly links to loneliness, behavioural problems, and negative academic outcomes.
2. "Latchkey children" refers to children who routinely return home from school to empty homes and take care of themselves for extended periods of time.
3. Although self-care generally points to negative outcomes, it is important to consider that the bulk of research has yet to track long-term consequences.
4. In research and practice, the phrase "children in self-care" has come to replace latchkey in an effort to more accurately reflect the nature of their circumstances.
5. Although parents might believe that self-care would be beneficial for development, recent research has found quite the opposite.
Five jumbled up sentences (labelled 1, 2, 3, 4 and 5), related to a topic, are given below. Four of them can be put together to form a coherent paragraph. Identify the odd sentence.
- The banning of Northern Lights could be considered a precursor to censoring books for “moral”, world view or religious reasons.
- Attempts to ban books are attempts to silence authors who have summoned immense courage in telling their stories.
- Now the banning and challenging of books in the US has escalated to an unprecedented level.
- The widely acclaimed fantasy novel Northern Lights was banned in some parts of the US, and was the second most challenged book in the US.
- The American Library Association documented an unparalleled number of reported book challenges in 2022, about 2,500 unique titles.
The four sentences (labelled 1, 2, 3 and 4) given below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer.
- Contemporary African writing like ‘The Bottled Leopard’ voices this theme using two children and two backgrounds to juxtapose two varying cultures.
- Chukwuemeka Ike explores the conflict, and casts the Western tradition as condescending, enveloping and unaccommodating towards local African practice.
- However, their views contradict the reality, for a rich and sustaining local African cultural ethos exists for all who care, to see and experience.
- Western Christian concepts tend to deny or feign ignorance about the existence of a genuine and enduring indigenous African tradition.
The four sentences (labelled 1, 2, 3 and 4) given below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer.
- Like the ants that make up a colony, no single neuron holds complex information like self-awareness, hope or pride.
- Although the human brain is not yet understood enough to identify the mechanism by which emergence functions, most neurobiologists agree that complex interconnections among the parts give rise to qualities that belong only to the whole.
- Nonetheless, the sum of all neurons in the nervous system generate complex human emotions like fear and joy, none of which can be attributed to a single neuron.
- Human consciousness is often called an emergent property of the human brain.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Heatwaves are becoming longer, frequent and intense due to climate change. The impacts of extreme heat are unevenly experienced; with older people and young children, those with pre-existing medical conditions and on low incomes significantly more vulnerable. Adaptation to heatwaves is a significant public policy concern. Research conducted among at-risk people in the UK reveals that even vulnerable people do not perceive themselves as at risk of extreme heat; therefore, early warnings of extreme heat events do not perform as intended. This suggests that understanding how extreme heat is narrated is very important. The news media play a central role in this process and can help warn people about the potential danger, as well as about impacts on infrastructure and society.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
People spontaneously create counterfactual alternatives to reality when they think “if only” or “what if” and imagine how the past could have been different. The mind computes counterfactuals for many reasons. Counterfactuals explain the past and prepare for the future, they implicate various relations including causal ones, and they affect intentions and decisions. They modulate emotions such as regret and relief, and they support moral judgments such as blame. The ability to create counterfactuals develops throughout childhood and contributes to reasoning about other people's beliefs, including their false beliefs.
Let a, b, m and n be natural numbers such that a > 1 and b > 1. If ambn = 144145, then the largest possible value of n - m is
The sum of all possible values of x satisfying the equation 24x2 - 22x2 + x + 16 + 22x + 30 = 0, is
For any natural numbers m, n, and k, such that k divides both m + 2n and 3m + 4n, k must be a common divisor of
Any non-zero real numbers x, y such that y ≠ 3 and 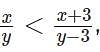 will satisfy the condition
will satisfy the condition
For some positive real number x, if 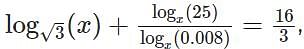 then the value of
then the value of 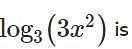
The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is
|
16 videos|27 docs|58 tests
|
|
16 videos|27 docs|58 tests
|