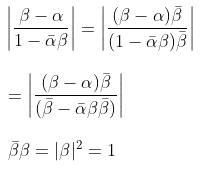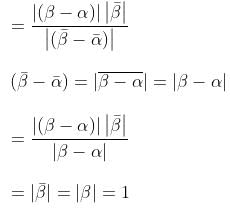Test: CAT Quantitative Aptitude- 7 - CAT MCQ
22 Questions MCQ Test CAT Mock Test Series 2025 - Test: CAT Quantitative Aptitude- 7
The question is followed by two statements, I and II. Answer each question using the following instructions: Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using both the statements together.
Mark (4) if the question can be answered by using either of the statements.
Is xy < 5?
I. x < 3 andy < 3 II. 1/2 < x < 2/3 and y2< 16
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using both the statements together.
Mark (4) if the question can be answered by using either of the statements.
Is xy < 5?
I. x < 3 andy < 3 II. 1/2 < x < 2/3 and y2< 16
Find the sum of all the natural numbers between 1 and 100, which are divisible by 3.
Krunal played 11 matches in Indian Cricket T-20 championship. Average runs scored by him in 11 matches was 16. His runs scored in nth match was 2 less than that of the (n - l)th match. Find the average runs scored by him in third and ninth match.
A boat takes 5 hours to row downstream along the entire length of the river. If the speed of the stream increases by 1 km/hr and the speed of the boat remains the same, the boat will take 40 hours to row upstream along the entire length of the river. If the speed of boat in still water is 5 km/hr, find the length of the river (in km).
What is the probability of occurrence of leap year having 53 Sundays ?
A certain shipping company has a certain free baggage allowance for each voyager. It charges for excess baggage at a fixed rate per kg. 2 voyagers, Mr. P and Mr. Q, have a total of 50 kg of baggage between them. They were charged Rs. 2,800 and Rs. 1,400, respectively for excess baggage. If the free baggage allowance were halved and the entire baggage belonged to one of them, then the excess baggage charge would have been Rs. 6,300. Find the weight (in kg) of Mr. P's baggage.
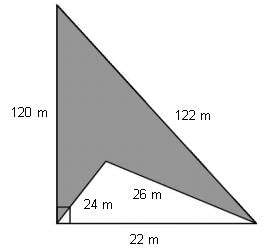
Calculate the area(in sq. m) of the shaded region in the following figure:(Type your answer to the nearest integer)
Forth and fifth terms of a series in geometric progression are 378 and 1134 respectively. What is the first term of the series?
In an examination, Jack scored 55 marks and Jill scored 30 more marks than Jack in the same examination. For every correct answer, a student gets 1 mark, but the negative marks per wrong answer for the first 20 wrong answers is different from that for the remaining wrong answers. Jack and Jill attempted 160 and 150 questions, respectively. If Jack and Jill correctly answered half and two third of the questions that they attended, respectively, then find the negative mark for each wrong answer beyond the first 20 wrong answers.
(Enter your answer rounded to two decimal places)
Each angle of a regular r-sided polygon is  times each angle of a regular s-sided polygon. What is the largest possible value of s?
times each angle of a regular s-sided polygon. What is the largest possible value of s?
The ratio of the cost price of cookie A to that of cookie B is 2 : 5. The ratio of profits made on selling the cookies is in the ratio 4 : 5. If the selling price of cookie B is Rs. 100, find the selling price of cookie A.
A man standing at the bottom of a hill wants to reach the top, which is at a distance of 10√13 km from him. He starts climbing at an angle of 30°. After sometime he finds that he is 10 km above ground level and decides to climb the remaining distance at an angle of 60°. What is the height of the hill?
Between 1 and 31, 'm' arithmetic means have been inserted in such a way that the ratio of the 7th and (m - 1)th means is 5 : 9, respectively. Find the value of m
Slant height of the cone is 25 cm. Diameter of the cone is 3/2 times the height of the cone. Find the volume of the cone (in cm3).
Each question is followed by two statements, I and II. Answer each question 3 using the following instructions: Marks Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements. Find the area of the triangle. (Enter the correct answer option.)
I. The measures of the sides of the triangle are in arithmetic progression.
II. The ratio of the sides is 2 : 3 : 4.
For which of the following functions f is f(x) = - f (1 +x) satisfies for all x?
A solid cylinder is immersed in a hemispherical bowl filled with water. What is the maximum volume of the liquid (in cubic units) that can be displaced, if the height of the cylinder is equal to the radius of the hemispherical bowl (given by r) and the radius of the cylinder is one third that of the bowl if cylinder is placed vertically?
If  and
and  are different complex numbers with
are different complex numbers with  = 1, find the value of
= 1, find the value of  .
.
A shopkeeper buys certain goods at 20% discount from the wholesaler. The shopkeeper then marks a price on the goods that would fetch him 50% profit. What percentage discount should he offer on this marked price so that he sells the goods at the marked price of the wholesaler (i.e., the price at which the wholesaler usually sells his goods) ?
In a class of 120 students, for every 2 students taking up Physics there are 4 students taking up Chemistry. Further for every student taking Physics there are 3 students taking up Maths as well as 1 student taking up Biology. Then the maximum number of students taking up all the four subjects will be:
Everday, Murugan starts at 4:00 pm from his home to pick up his son from school. They reach house at 6:00 pm. One day, school was over at 4:00 pm and Murugan, not aware of this, started from home as usual. He met his son on the way and they reached home 20 minutes earlier than usual. If the speed of the car is 30 km/hr, find his son's speed (in km/hr).
A lattice point (x, y) in the rectangular coordinate plane is a point in which both x and y are integers. How many lattice points are there in the interior of the circle x2 + y2 = 11?
|
25 videos|32 docs|70 tests
|


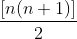
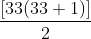 = 561
= 561
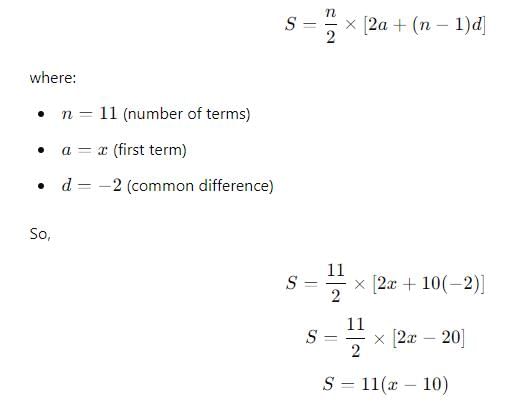

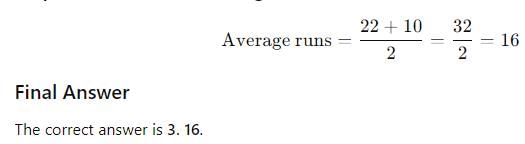
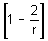 and 180°
and 180°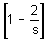 .
.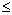 117.
117.