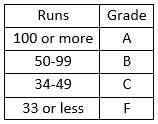
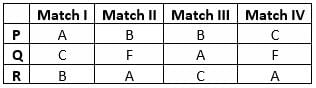
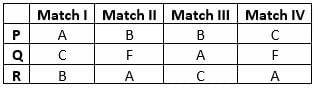
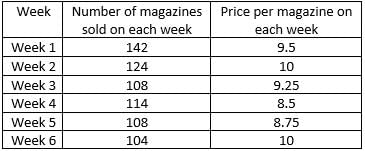
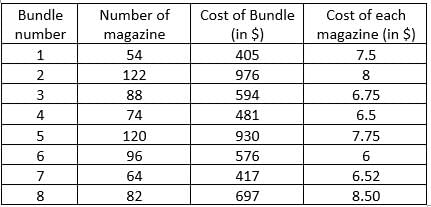
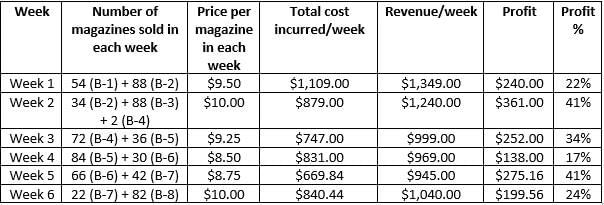
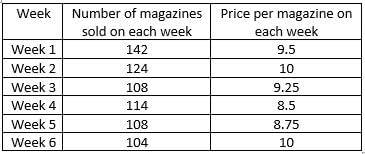
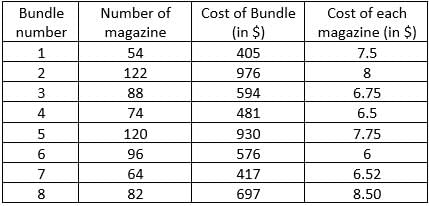
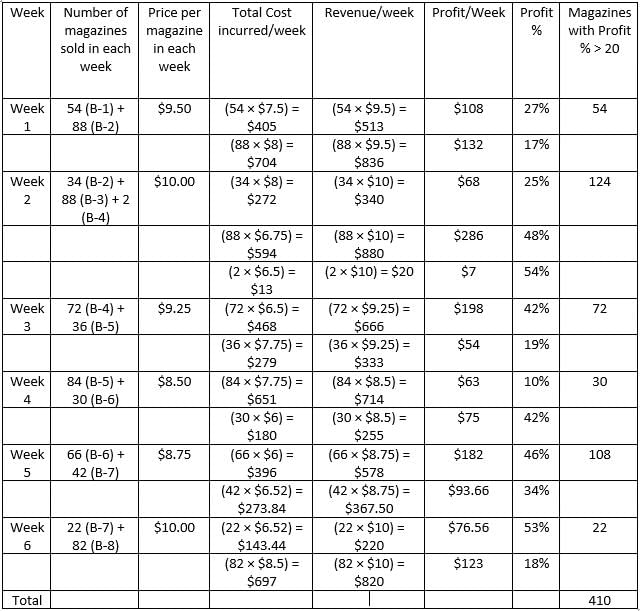
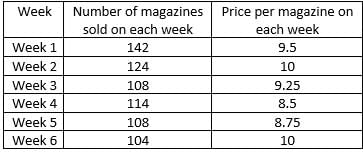
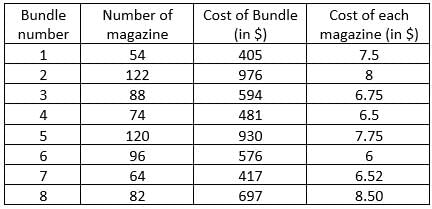
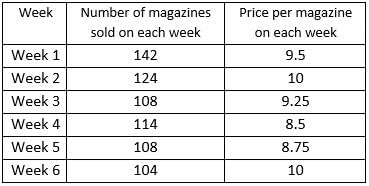
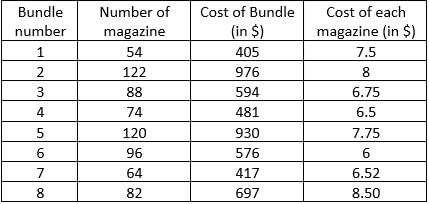
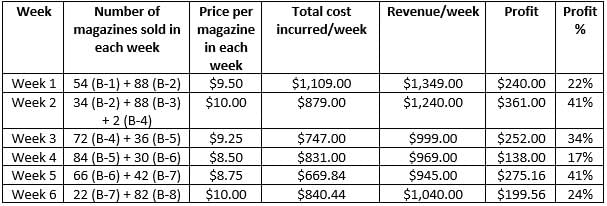
Step 1: Apply Condition II
The student who missed the Mathematics examination did not miss any other examination.
Therefore, their Mathematics score must be equal to the average of the best 3 out of the 4 exam scores obtained.
Step 2: Eliminate impossible cases
-
If a student’s Mathematics score is greater than all other exam scores, it cannot be the average.
-
Thus, Deep and Esha can be eliminated immediately.
Step 3: Check each remaining candidate
-
Alva
Best 3 scores = English (80), Hindi (75), Science (75)
Average = (80 + 75 + 75) ÷ 3 = 230 ÷ 3 = 76.67
Mathematics score = 70 → Not matching -
Carl
Best 3 scores = Hindi (80), Social Science (90), Science (100)
Average = (80 + 90 + 100) ÷ 3 = 270 ÷ 3 = 90
Mathematics score = 90 → Matching -
Foni
Best 3 scores = English (83), Social Science (83), Science (88)
Average = (83 + 83 + 88) ÷ 3 = 254 ÷ 3 = 84.67
Mathematics score = 78 → Not matching
Step 4: Conclusion
Only Carl’s Mathematics score matches the required condition.
Final Answer
Carl most likely missed his Mathematics examination.