Test: CAT Logical Reasoning & Data Interpretation- 3 - CAT MCQ
20 Questions MCQ Test - Test: CAT Logical Reasoning & Data Interpretation- 3
Which of the following is the least number of wins that the winner of the world championship can have?
Which of the following is the maximum number of wins that a player could have had and still not be selected for the world championship tournament?
Which of the following is the least number of wins one needs to enter the world championship?
After all the five tournaments, a table was made of the players in the descending order of their wins in all the five tournaments combined. What is the maximum number of wins the top four players could have got if no player among the 128 participants won more than one tournament?
If they start from Paris at 8:00 PM, what is the average time taken by them to travel from Paris to Luxembourg in their first 80 trips?
If they start at 6:00 AM from Luxembourg, what is the average time per trip for their first 25 trips?
If they start at 4:00 AM from Paris, after a minimum of how many trips (including the first one) will they start from Luxembourg at 8:00 AM?
If they start at 2: 00 PM from Luxembourg, how many times will they start between 1:00 PM and 11:00 PM from Paris in their first 100 trips?
From which club did maximum number of people leave for the dramatics club?
How many persons moved from the sports club to quiz club?
What is the absolute difference between the number of students who joined literary club and the number of students who left it?
The strength of which club decreased the most after the change?
How many codes are possible if all the digits from A to H are greater than 4?
Which of the following statements cannot be true?
What is the absolute difference between the number of valid codes and invalid codes among the ones given below?
22666689
33996656
99999912
22469234
55555556
44848434
22489667
33333332
44888845
Which of the following must be true?
How many codes are possible such that each digit from A to H is necessarily prime?
Which of the following is a plausible performance sequence?
How many codes are possible?
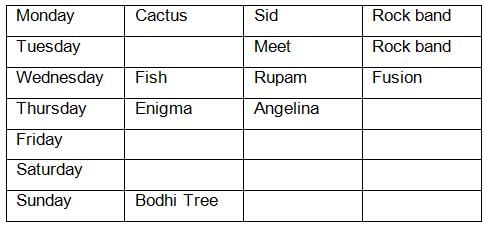
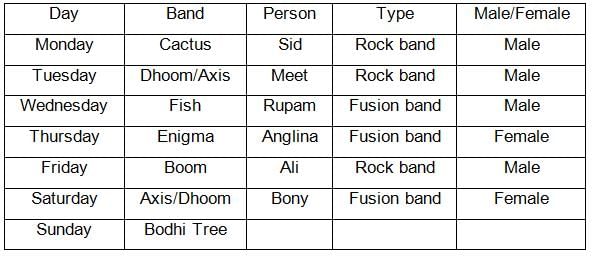
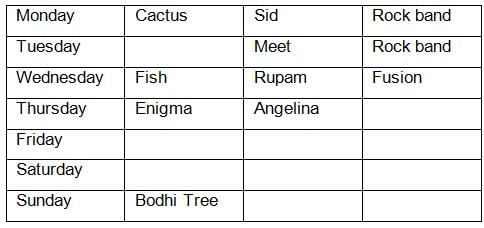
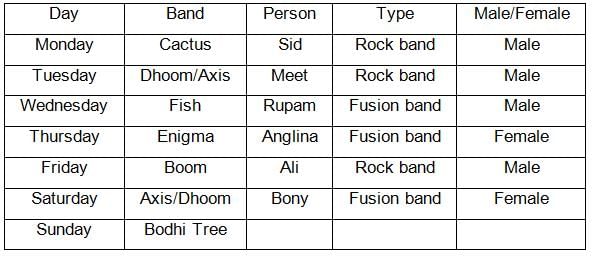
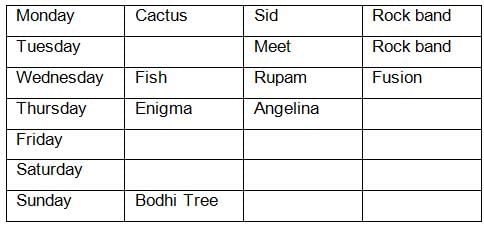
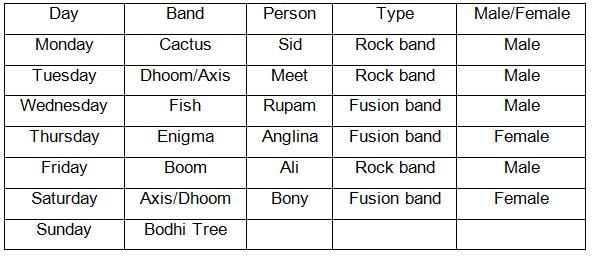
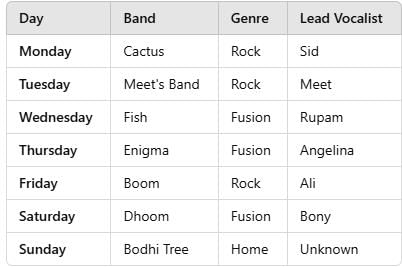
How many times from Monday to Saturday did the fusion band and rock band perform consecutively?