All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  CAT Mock Test Series 2024  >  Test: CAT Logical Reasoning & Data Interpretation- 4 - CAT MCQ

Test: CAT Logical Reasoning & Data Interpretation- 4 - CAT MCQ


Test Description

20 Questions MCQ Test CAT Mock Test Series 2024 - Test: CAT Logical Reasoning & Data Interpretation- 4

Test: CAT Logical Reasoning & Data Interpretation- 4 for CAT 2024 is part of CAT Mock Test Series 2024 preparation. The Test: CAT Logical Reasoning & Data Interpretation- 4 questions and answers have been prepared according to the CAT exam syllabus.The Test: CAT Logical Reasoning & Data Interpretation- 4 MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: CAT Logical Reasoning & Data Interpretation- 4 below.
Solutions of Test: CAT Logical Reasoning & Data Interpretation- 4 questions in English are available as part of our CAT Mock Test Series 2024 for CAT & Test: CAT Logical Reasoning & Data Interpretation- 4 solutions in Hindi for CAT Mock Test Series 2024 course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: CAT Logical Reasoning & Data Interpretation- 4 | 20 questions in 40 minutes | Mock test for CAT preparation | Free important questions MCQ to study CAT Mock Test Series 2024 for CAT Exam | Download free PDF with solutions
*Answer can only contain numeric values
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 1
Save

What is the registration number of white car?


Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 1

The registration number of white car is 1115.

Given that the registration number of white car has less than 3 different digits. It cannot have only one digit (since no digit occurs 4 times). Hence, the registration number of white car must be a multiple of 5 (i.e. end in a 0 or a 5) and have 2 different digits, i.e. be of the form (aaab/abbb) OR (aabb). Hence, 3a + b = 8 (for which the only possibility is a = 1 and b = 5, since 0 appears only twice) or 2a + 2b = 8 (for which there is no possibility, since 4 does not appear even once and at least one of a and b must be 0 or 5). Hence. only 1115 is possible.

The registration number of white car is exactly a factor of registration number of black car or we can say that the registration number of black car is a multiple of registration number of white car. Multiples of 1115 with four digits are 2230, 3345, 4460, 5575, 6690, 7805 and 8920. Of these, only 6690 is possible (8920 and 7805 are not possible because the registration number of red car should have three digits, which are not in anyone else's registration number, i.e. the registration number of red car should have three digits out of 2, 7, 8 and 9).

Since 9 is present in the registration number of black car, red car's registration number should contain 2, 7, 8 and 5/0. The registration number of grey car will have the digits 3, 3, 5 and 5/0. But, if there are two 5s in the registration number of grey car, it will not have at least three distinct digits. Hence, the registration number of grey car will have the digits 3, 3, 5 and 0 and the registration number of red car will be either 2785 or 2875.

From (5), 2785 + 500 = 3285 and 2875 + 500 = 3375. The registration number of grey car should lie between 3285 and 3475. The only possible values of registration number of grey car are 3350 and 3305. Since both these values are less than 3375, the registration number of red car cannot be 2875. Therefore, the registration number of red car must be 2785 and the registration number of grey car can be 3350 or 3305.

*Answer can only contain numeric values
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 2
Save

How many of the four cars have a registration number which is a multiple of 3? Key in the correct value.


Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 2

Only the registration number of black car i.e.6690 is a multiple of 3.

Given that the registration number of white car has less than 3 different digits. It cannot have only one digit (since no digit occurs 4 times). Hence, the registration number of white car must be a multiple of 5 (i.e. end in a 0 or a 5) and have 2 different digits, i.e. be of the form (aaab/abbb) OR (aabb). Hence, 3a + b = 8 (for which the only possibility is a = 1 and b = 5, since 0 appears only twice) or 2a + 2b = 8 (for which there is no possibility, since 4 does not appear even once and at least one of a and b must be 0 or 5). Hence. only 1115 is possible.

The registration number of white car is exactly a factor of registration number of black car or we can say that the registration number of black car is a multiple of registration number of white car. Multiples of 1115 with four digits are 2230, 3345, 4460, 5575, 6690, 7805 and 8920. Of these, only 6690 is possible (8920 and 7805 are not possible because the registration number of red car should have three digits, which are not in anyone else's registration number, i.e. the registration number of red car should have three digits out of 2, 7, 8 and 9).

Since 9 is present in the registration number of black car, red car's registration number should contain 2, 7, 8 and 5/0. The registration number of grey car will have the digits 3, 3, 5 and 5/0. But, if there are two 5s in the registration number of grey car, it will not have at least three distinct digits. Hence, the registration number of grey car will have the digits 3, 3, 5 and 0 and the registration number of red car will be either 2785 or 2875.

From (5), 2785 + 500 = 3285 and 2875 + 500 = 3375. The registration number of grey car should lie between 3285 and 3475. The only possible values of registration number of grey car are 3350 and 3305. Since both these values are less than 3375, the registration number of red car cannot be 2875. Therefore, the registration number of red car must be 2785 and the registration number of grey car can be 3350 or 3305.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 3
Save

What is the sum of registration numbers of red car and black car?

Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 3

The sum of the registration numbers of red car and black car is 9475.

Given that the registration number of white car has less than 3 different digits. It cannot have only one digit (since no digit occurs 4 times). Hence, the registration number of white car must be a multiple of 5 (i.e. end in a 0 or a 5) and have 2 different digits, i.e. be of the form (aaab/abbb) OR (aabb). Hence, 3a + b = 8 (for which the only possibility is a = 1 and b = 5, since 0 appears only twice) or 2a + 2b = 8 (for which there is no possibility, since 4 does not appear even once and at least one of a and b must be 0 or 5). Hence. only 1115 is possible.

The registration number of white car is exactly a factor of registration number of black car or we can say that the registration number of black car is a multiple of registration number of white car. Multiples of 1115 with four digits are 2230, 3345, 4460, 5575, 6690, 7805 and 8920. Of these, only 6690 is possible (8920 and 7805 are not possible because the registration number of red car should have three digits, which are not in anyone else's registration number, i.e. the registration number of red car should have three digits out of 2, 7, 8 and 9).

Since 9 is present in the registration number of black car, red car's registration number should contain 2, 7, 8 and 5/0. The registration number of grey car will have the digits 3, 3, 5 and 5/0. But, if there are two 5s in the registration number of grey car, it will not have at least three distinct digits. Hence, the registration number of grey car will have the digits 3, 3, 5 and 0 and the registration number of red car will be either 2785 or 2875.

From (5), 2785 + 500 = 3285 and 2875 + 500 = 3375. The registration number of grey car should lie between 3285 and 3475. The only possible values of registration number of grey car are 3350 and 3305. Since both these values are less than 3375, the registration number of red car cannot be 2875. Therefore, the registration number of red car must be 2785 and the registration number of grey car can be 3350 or 3305.

*Answer can only contain numeric values
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 4
Save

If two out of the four registration numbers are multiples of 10, then what is the registration number of grey car?

Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 4

It is given that the registration number of white car has less than 3 different digits. It cannot have only one digit (since no digit occurs 4 times). Hence, the registration number of white car must be a multiple of 5 (i.e. end in a 0 or a 5) and have 2 different digits, i.e. be of the form (aaab/abbb) OR (aabb). Hence, 3a + b = 8 (for which the only possibility is a = 1 and b = 5, since 0 appears only twice) or 2a + 2b = 8 (for which there is no possibility, since 4 does not appear even once and at least one of a and b must be 0 or 5). Hence, only 1115 is possible.

The registration number of white car is exactly a factor of the registration number of black car or we can say that the registration number of black car is a multiple of the registration number of white car. Multiples of 1115 with four digits are 2230, 3345, 4460, 5575, 6690, 7805 and 8920. Of these, only 6690 is possible (8920 and 7805 are not possible because the registration number of red car should have three digits, which are not in anyone else's registration number, i.e. the registration number of red car should have three digits out of 2, 7, 8 and 9).

Since 9 is present in the registration number of black car, red car's registration number should contain 2, 7, 8 and 5/0. The registration number of grey car will have the digits 3, 3, 5 and 5/0, but if there are two 5s in the registration number of grey car, it will not have at least three distinct digits. Hence, the registration number of grey car will have the digits 3, 3, 5 and 0 and the registration number of red car will be either 2785 or 2875.

From (5), 2785 + 500 = 3285 and 2875 + 500 = 3375. The registration number of grey car should lie between 3285 and 3475. The only possible values of the registration number of grey car are 3350 and 3305. Since both these values are less than 3375, the registration number of red car cannot be 2875. Therefore, the registration number of red car must be 2785 and the registration number of grey car can be 3350 or 3305.

*Answer can only contain numeric values
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 5
Save

How many cars have a registration number with either of the middle two digits same as either of the extreme two digits?

Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 5

It is given that the registration number of white car has less than 3 different digits. It cannot have only one digit (since no digit occurs 4 times). Hence, the registration number of white car must be a multiple of 5 (i.e. end in a 0 or a 5) and have 2 different digits, i.e. be of the form (aaab/abbb) OR (aabb). Hence, 3a + b = 8 (for which the only possibility is a = 1 and b = 5, since 0 appears only twice) or 2a + 2b = 8 (for which there is no possibility, since 4 does not appear even once and at least one of a and b must be 0 or 5). Hence, only 1115 is possible.
The registration number of white car is exactly a factor of the registration number of black car or we can say that the registration number of black car is a multiple of the registration number of white car. Multiples of 1115 with four digits are 2230, 3345, 4460, 5575, 6690, 7805 and 8920. Of these, only 6690 is possible (8920 and 7805 are not possible because the registration number of red car should have three digits, which are not in anyone else's registration number, i.e. the registration number of red car should have three digits out of 2, 7, 8 and 9).
Since 9 is present in the registration number of black car, red car's registration number should contain 2, 7, 8 and 5/0. The registration number of grey car will have the digits 3, 3, 5 and 5/0, but if there are two 5s in the registration number of grey car, it will not have at least three distinct digits. Hence, the registration number of grey car will have the digits 3, 3, 5 and 0 and the registration number of red car will be either 2785 or 2875.
From (5), 2785 + 500 = 3285 and 2875 + 500 = 3375. The registration number of grey car should lie between 3285 and 3475. The only possible values of the registration number of grey car are 3350 and 3305. Since both these values are less than 3375, the registration number of red car cannot be 2875. Therefore, the registration number of red car must be 2785 and the registration number of grey car can be 3350 or 3305.

Only in the case of Red car (Registration number: 2785) , neither of the middle 2 digits is the same as either of the extreme 2 digits.

*Answer can only contain numeric values
Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 6
Save

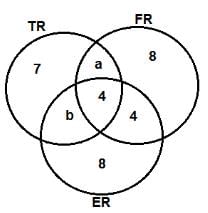
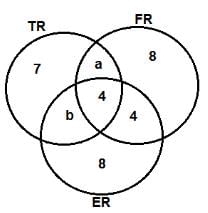
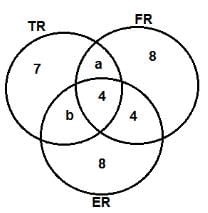
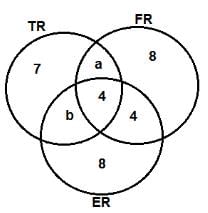
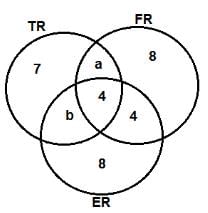
Based on the given information, the least number of volunteers involved in both the FR and TR projects but not in the ER project is __________.

Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 6
  • A total of 17 volunteers are involved in the TR project and 10 in TR are also involved in other projects. Thus, 7 volunteers are involved only in TR.
  • The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in the ER project alone. Eight volunteers are involved in ER alone.
  • The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects. So, 4 volunteers are involved in all the three projects.
  • Among them, the number of volunteers involved in the FR project alone is equal to the number of volunteers having involvement in the ER project alone. So, 8 volunteers are involved in FR alone.
  • Let number of volunteers involved in both TR and FR but not ER = a

Number of volunteers involved in both TR and ER but not FR = b
a + b + 4 = 10
a + b = 6
Let number of volunteers involved in both FR and ER but not TR = x
Total = 17 + x + 8 + 8 = 37
x = 4
Consider the Venn diagram shown below:

Number of volunteers involved in FR > Number of volunteers involved in TR
Number of volunteers involved in FR > Number of volunteers involved in ER
∴ 16 + a > 17 and 16 + a > 16 + b or a > b
∴ a and b can be (6, 0), (5, 1), or (4, 2).
Least number of volunteers involved in both the FR and TR projects but not in the ER project = Least value of a = 4

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 7
Save

Which of the following additional pieces of information would enable to find the exact number of volunteers involved in the various projects?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 7
  • A total of 17 volunteers are involved in the TR project and 10 in TR are also involved in other projects. Thus, 7 volunteers are involved only in TR.
  • The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in the ER project alone. Eight volunteers are involved in ER alone.
  • The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects. So, 4 volunteers are involved in all the three projects.
  • Among them, the number of volunteers involved in the FR project alone is equal to the number of volunteers having involvement in the ER project alone. So, 8 volunteers are involved in FR alone.
  • Let number of volunteers involved in both TR and FR but not ER = a

Number of volunteers involved in both TR and ER but not FR = b
a + b + 4 = 10
a + b = 6
Let number of volunteers involved in both FR and ER but not TR = x
Total = 17 + x + 8 + 8 = 37
x = 4
Consider the Venn diagram shown below:

We can obtain the information in options 2 and 3 from the data given in the passage.
The information in option 1 will give us the value of a, which in turn will give us the value of b. Thus, option 1 would enable us to find the exact number of volunteers involved in the various projects.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 8
Save

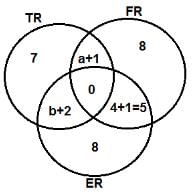
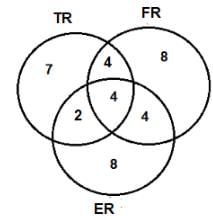
Which of the following statements necessarily follows after this rearrangement?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 8
  • A total of 17 volunteers are involved in the TR project and 10 in TR are also involved in other projects. Thus, 7 volunteers are involved only in TR.
  • The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in the ER project alone. Eight volunteers are involved in ER alone.
  • The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects. So, 4 volunteers are involved in all the three projects.
  • Among them, the number of volunteers involved in the FR project alone is equal to the number of volunteers having involvement in the ER project alone. So, 8 volunteers are involved in FR alone.
  • Let number of volunteers involved in both TR and FR but not ER = a

Number of volunteers involved in both TR and ER but not FR = b
a + b + 4 = 10
a + b = 6
Let number of volunteers involved in both FR and ER but not TR = x
Total = 17 + x + 8 + 8 = 37
x = 4
Consider the Venn diagram shown below:

Number of volunteers involved in FR > Number of volunteers involved in ER
16 + a > 16 + b
a and b can be (6, 0), (5, 1), or (4, 2).
After the volunteers withdraw as mentioned, the number of volunteers working on different projects is as shown below:

After the volunteers withdraw as mentioned,

  • Number of volunteers working on TR = 7 + 6 + 3 = 16
  • Number of volunteers working on FR = 14 + a
  • Number of volunteers working on ER = 15 + b

From options:

1. The lowest number of volunteers is now in the TR project.
Incorrect: For b = 0, Number of volunteers working on ER = 15
2. More volunteers are now in the ER project as compared to the TR project.
Incorrect: For b = 0, Number of volunteers working on ER = 15
3. More volunteers are now in the TR project as compared to the ER project.
Incorrect: For b = 2, Number of volunteers working on ER = 17
4. More volunteers are now in the FR project as compared to the ER project.
Correct for all possible value of a and b: 14 + a > 15 + b
(a, b) = (6, 0), (5, 1), (4, 2)
∴ More volunteers are now in FR than in ER.
Therefore, option 4 is the correct answer.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 9
Save

Which of the projects now has the highest number of volunteers?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 9
  • A total of 17 volunteers are involved in the TR project and 10 in TR are also involved in other projects. Thus, 7 volunteers are involved only in TR.
  • The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in the ER project alone. Eight volunteers are involved in ER alone.
  • The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects. So, 4 volunteers are involved in all the three projects.
  • Among them, the number of volunteers involved in the FR project alone is equal to the number of volunteers having involvement in the ER project alone. So, 8 volunteers are involved in FR alone.
  • Let number of volunteers involved in both TR and FR but not ER = a

Number of volunteers involved in both TR and ER but not FR = b
a + b + 4 = 10
a + b = 6
Let number of volunteers involved in both FR and ER but not TR = x
Total = 17 + x + 8 + 8 = 37
x = 4
Consider the Venn diagram shown below:

Let m volunteers be added to the TR project and n be added to each of the FR and ER projects.
Then, 7 + m = 8 + n
m = n + 1
Also, b + 2 = 5
∴ b = 3 and a = 3
Number of volunteers working on TR = 7 + n + 1 + 4 + 5 = 17 + n
Number of volunteers working on FR = 17 + n
Number of volunteers working on ER = 18 + n
Thus, ER has the highest number of volunteers.
Hence, option 4 is the correct choice.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 10
Save

Which of the following is true?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 10
  • A total of 17 volunteers are involved in the TR project and 10 in TR are also involved in other projects. Thus, 7 volunteers are involved only in TR.
  • The number of volunteers involved in the TR project alone is one less than the number of volunteers involved in the ER project alone. Eight volunteers are involved in ER alone.
  • The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects. So, 4 volunteers are involved in all the three projects.
  • Among them, the number of volunteers involved in the FR project alone is equal to the number of volunteers having involvement in the ER project alone. So, 8 volunteers are involved in FR alone.
  • Let number of volunteers involved in both TR and FR but not ER = a

Number of volunteers involved in both TR and ER but not FR = b
a + b + 4 = 10
a + b = 6
Let number of volunteers involved in both FR and ER but not TR = x
Total = 17 + x + 8 + 8 = 37
x = 4
Consider the Venn diagram shown below:

Number of volunteers involved in FR > Number of volunteers involved in TR
Number of volunteers involved in FR > Number of volunteers involved in ER
∴ 16 + a > 17 and 16 + a > 16 + b or a > b
∴ a and b can be (6, 0), (5, 1), or (4, 2).
Maximum number of volunteers involved in both the FR and TR projects but not in the ER project = Maximum value of b = 2

Maximum total number of volunteers involved in ER = 2 + 4 + 4 + 8 = 18

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 11
Save

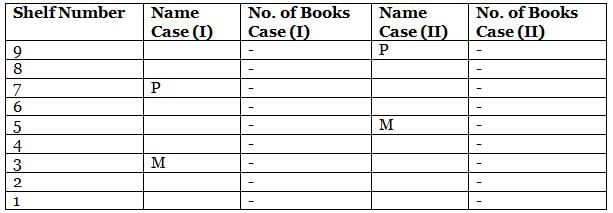
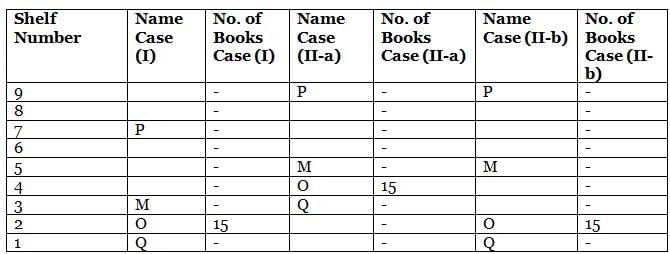
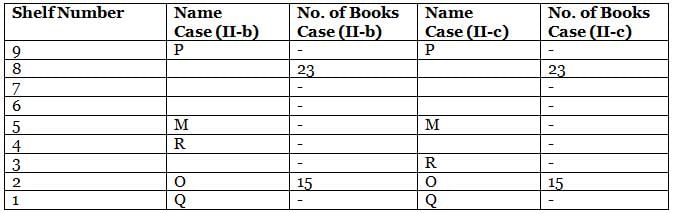
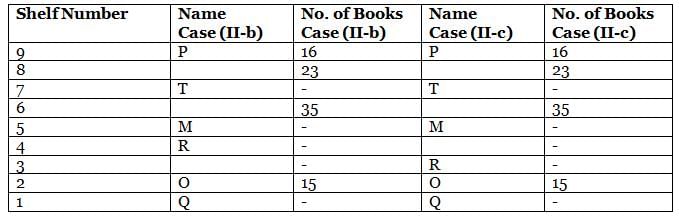
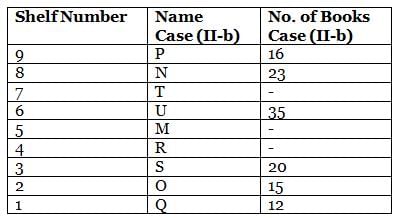
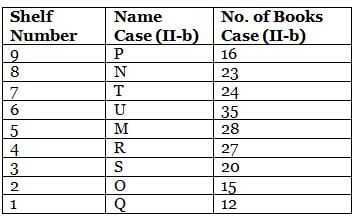
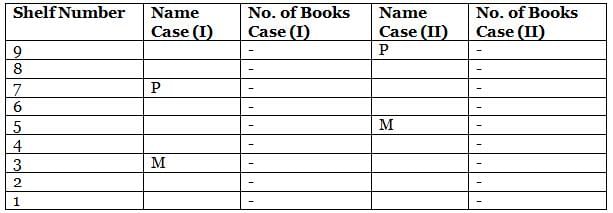
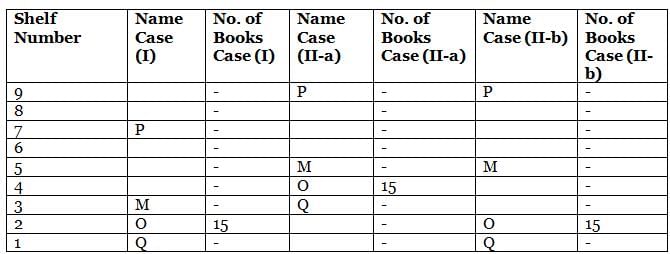
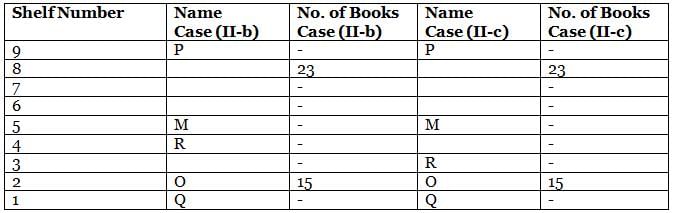
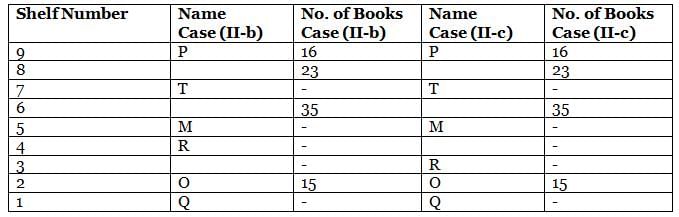
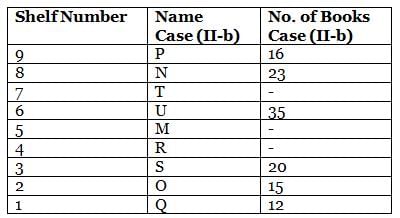
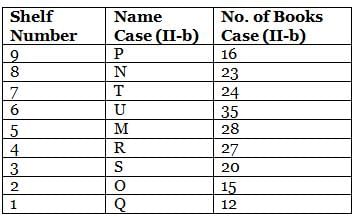
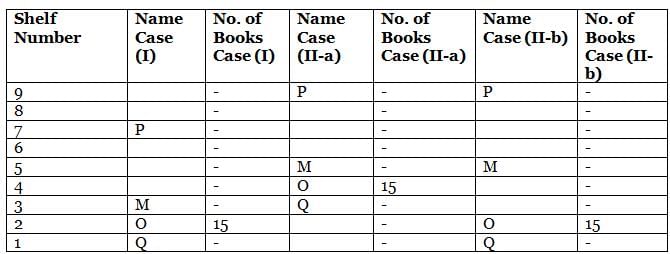
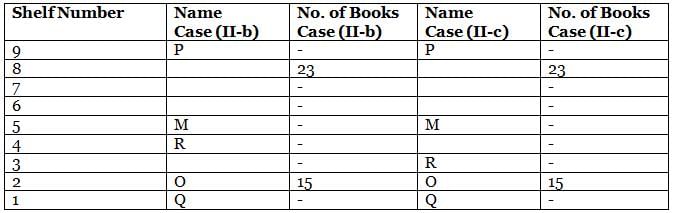
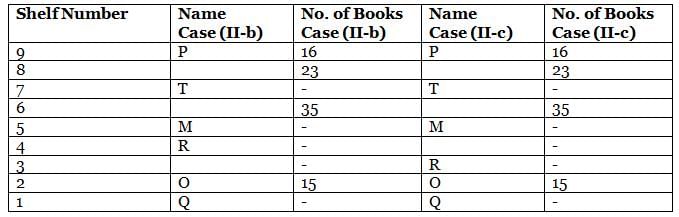
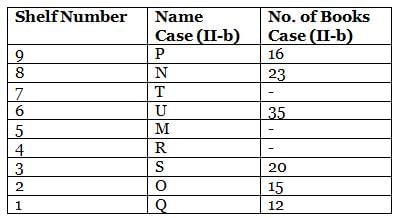
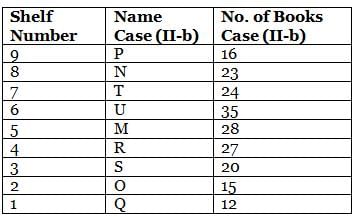
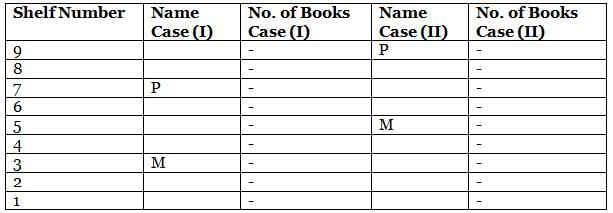
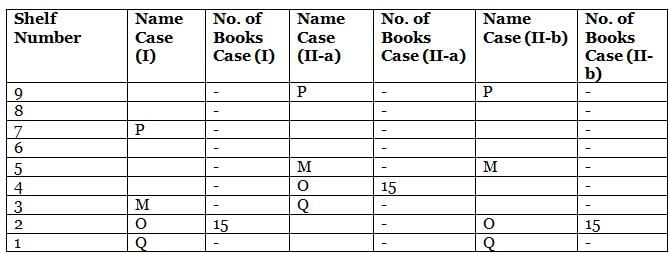
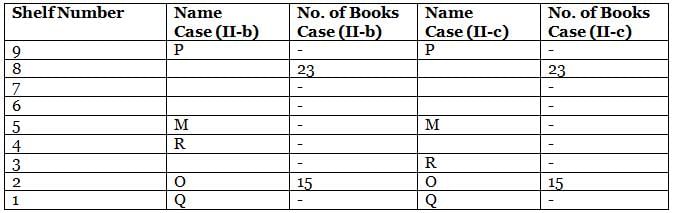
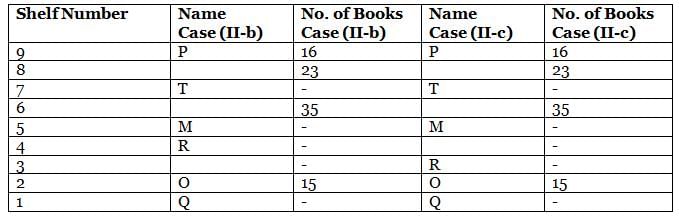
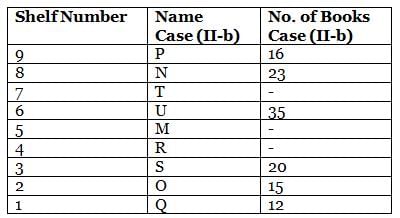
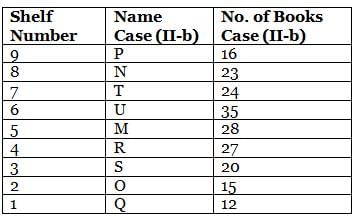
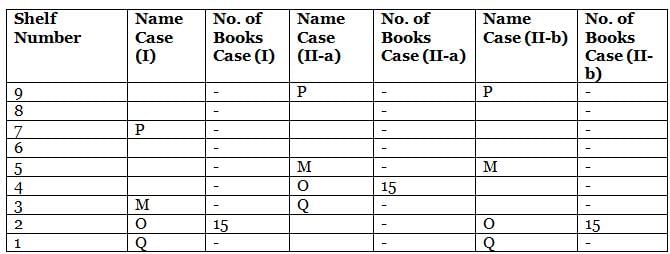
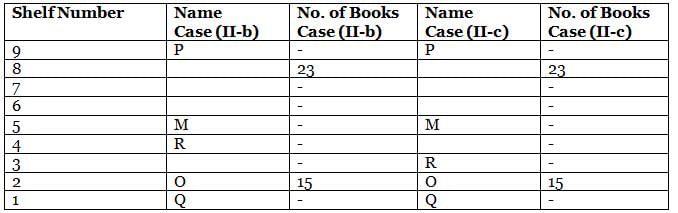
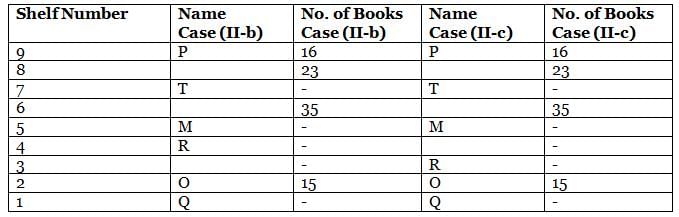
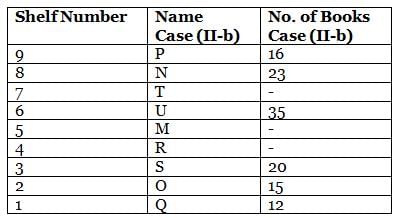
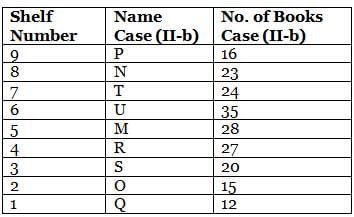
What is the total of the books on shelves 7 and 3?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 11

Shelf P contains even numbered books.
At least five shelves are below P.
There are three shelves between shelves M and P.

The total number of books on shelves P and Q is 28.
Therefore, Q contains even numbered books.
Shelf O has 15 books and is below M.
Q is either immediately below O or immediately above M.
Since Q has even numbered books, it cannot be immediately above M.

Shelf R is below M but not below Q. This cannot be true in cases (I) and (II-a).
There are two shelves between M and the shelf which contains 23 books.

P contains one more book than shelf 2.
Shelf T contains even numbered books and is not below R.
The total number of books on shelves 2, 8 and 6 is 73.

Shelf N contains odd numbered books which are less than 30.
Shelf S contains 3 less books than shelf 8.
This cannot be true in case (II-c).
Q contains the least number of books which is a multiple of 3.
Each shelf contains more than 10 books.
The number of books on shelf U is odd.

The difference between the number of books on Q and on T is 12.
The difference between the number of books on M and on R is 1.
The total number of books on shelves 5 and R is 55.

The final arrangement is thus as shown above.
From the above arrangement, it is evident that the total of the books on shelves 7 and 3 is 44.
Hence, answer option 2 is correct.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 12
Save

Which among the following shelves contains the most number of books?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 12

Shelf P contains even numbered books.
At least five shelves are below P.
There are three shelves between shelves M and P.

The total number of books on shelves P and Q is 28.
Therefore, Q contains even numbered books.
Shelf O has 15 books and is below M.
Q is either immediately below O or immediately above M.
Since Q has even numbered books, it cannot be immediately above M.

Shelf R is below M but not below Q. This cannot be true in cases (I) and (II-a).
There are two shelves between M and the shelf which contains 23 books.

P contains one more book than shelf 2.
Shelf T contains even numbered books and is not below R.
The total number of books on shelves 2, 8 and 6 is 73.

Shelf N contains odd numbered books which are less than 30.
Shelf S contains 3 less books than shelf 8.
This cannot be true in case (II-c).
Q contains the least number of books which is a multiple of 3.
Each shelf contains more than 10 books.
The number of books on shelf U is odd.

The difference between the number of books on Q and on T is 12.
The difference between the number of books on M and on R is 1.
The total number of books on shelves 5 and R is 55.

The final arrangement is thus as shown above.
From the above table it is evident that out of the given shelves, shelf U contains the most number of books.
Hence, answer option 4 is correct.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 13
Save

Find the odd one out.
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 13

Shelf P contains even numbered books.
At least five shelves are below P.
There are three shelves between shelves M and P.

The total number of books on shelves P and Q is 28.
Therefore, Q contains even numbered books.
Shelf O has 15 books and is below M.
Q is either immediately below O or immediately above M.
Since Q has even numbered books, it cannot be immediately above M.

Shelf R is below M but not below Q. This cannot be true in cases (I) and (II-a).
There are two shelves between M and the shelf which contains 23 books.

P contains one more book than shelf 2.
Shelf T contains even numbered books and is not below R.
The total number of books on shelves 2, 8 and 6 is 73.

Shelf N contains odd numbered books which are less than 30.
Shelf S contains 3 less books than shelf 8.
This cannot be true in case (II-c).
Q contains the least number of books which is a multiple of 3.
Each shelf contains more than 10 books.
The number of books on shelf U is odd.

The difference between the number of books on Q and on T is 12.
The difference between the number of books on M and on R is 1.
The total number of books on shelves 5 and R is 55.

The final arrangement is thus as shown above.
From the above given table it is evident that except R, all the other shelves are odd numbered and contain an even number of books.
Hence, answer option 3 is correct.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 14
Save

How many shelves are there between shelves T and 6?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 14

Shelf P contains even numbered books.
At least five shelves are below P.
There are three shelves between shelves M and P.

The total number of books on shelves P and Q is 28.
Therefore, Q contains even numbered books.
Shelf O has 15 books and is below M.
Q is either immediately below O or immediately above M.
Since Q has even numbered books, it cannot be immediately above M.

Shelf R is below M but not below Q. This cannot be true in cases (I) and (II-a).
There are two shelves between M and the shelf which contains 23 books.

P contains one more book than shelf 2.
Shelf T contains even numbered books and is not below R.
The total number of books on shelves 2, 8 and 6 is 73.

Shelf N contains odd numbered books which are less than 30.
Shelf S contains 3 less books than shelf 8.
This cannot be true in case (II-c).
Q contains the least number of books which is a multiple of 3.
Each shelf contains more than 10 books.
The number of books on shelf U is odd.

The difference between the number of books on Q and on T is 12.
The difference between the number of books on M and on R is 1.
The total number of books on shelves 5 and R is 55.

The final arrangement is thus as shown above.
From the above table it is evident that there is no shelf between shelves T and 6.
Hence, answer option 1 is correct.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 15
Save

How many shelves are there below shelf M?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 15

Shelf P contains even numbered books.
At least five shelves are below P.
There are three shelves between shelves M and P.

The total number of books on shelves P and Q is 28.
Therefore, Q contains even numbered books.
Shelf O has 15 books and is below M.
Q is either immediately below O or immediately above M.
Since Q has even numbered books, it cannot be immediately above M.

Shelf R is below M but not below Q. This cannot be true in cases (I) and (II-a).
There are two shelves between M and the shelf which contains 23 books.

P contains one more book than shelf 2.
Shelf T contains even numbered books and is not below R.
The total number of books on shelves 2, 8 and 6 is 73.

Shelf N contains odd numbered books which are less than 30.
Shelf S contains 3 less books than shelf 8.
This cannot be true in case (II-c).
Q contains the least number of books which is a multiple of 3.
Each shelf contains more than 10 books.
The number of books on shelf U is odd.

The difference between the number of books on Q and on T is 12.
The difference between the number of books on M and on R is 1.
The total number of books on shelves 5 and R is 55.

The final arrangement is thus as shown above.
From the above given table it is evident that there are four shelves below shelf M.
Hence, answer option 2 is correct.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 16
Save

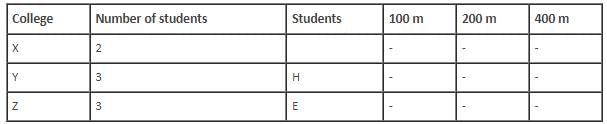
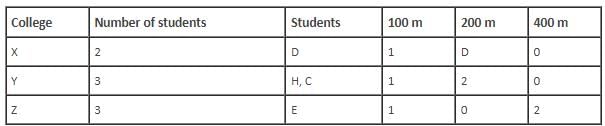
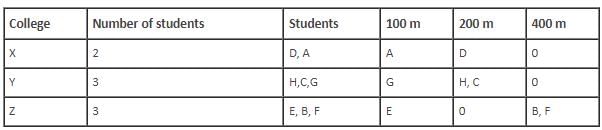
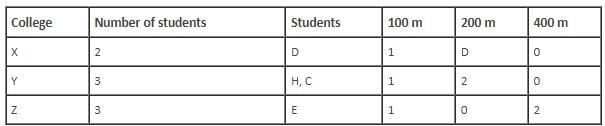
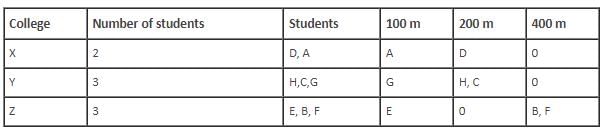
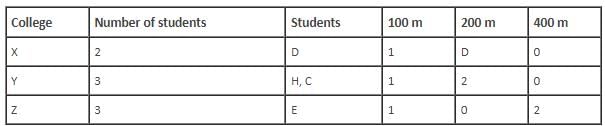
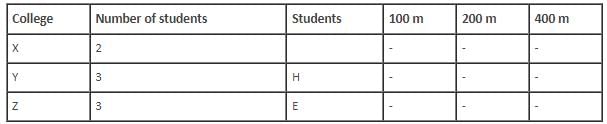
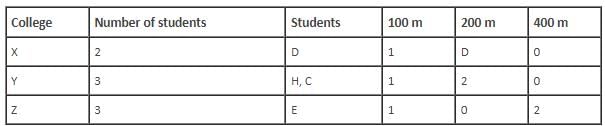
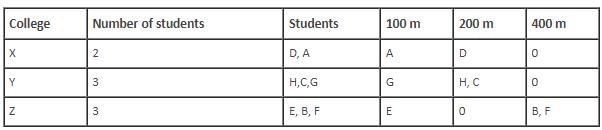
Who among the following is from college X?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 16

Number of students from college Y and Z are same. H is from college Y. E is from college Z. According to this information the following table is obtained.

D won medal in 200 m race event and he is not from college Y. No student from college Z has won medal in 200 m race event. Student from each college has won medal in 100 m race event. C is not from college Z nor he has won medal in 100 m race event. According to this the following table is obtained.

Number of students who won medals in 100 m race event is more than the number of students who won medals in 400 m race event. D and G are not from same college. All the medals of 400 m race event are won by students of same college. A and G won medals in same race event but they are not from same college. C is not from college Z nor he has won medal in 100 m race event. According to this the final table is shown below.

A is from college X.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 17
Save

Which of the following is a pair of students who are not from same college and neither have they won medals in the same race event?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 17

Number of students from college Y and Z are same. H is from college Y. E is from college Z. According to this information the following table is obtained.

D won medal in 200 m race event and he is not from college Y. No student from college Z has won medal in 200 m race event. Student from each college has won medal in 100 m race event. C is not from college Z nor he has won medal in 100 m race event. According to this the following table is obtained.

Number of students who won medals in 100 m race event is more than the number of students who won medals in 400 m race event. D and G are not from same college. All the medals of 400 m race event are won by students of same college. A and G won medals in same race event but they are not from same college. C is not from college Z nor he has won medal in 100 m race event. According to this the final table is shown below.

B is from college Z and has won medal in 400 m race whereas C is from college Y and won medal in 200 m race event.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 18
Save

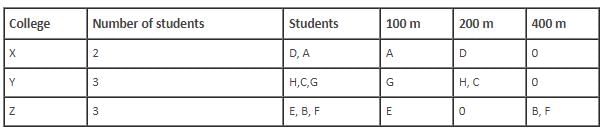
Which of the following statements is correct?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 18

Number of students from college Y and Z are same. H is from college Y. E is from college Z. According to this information the following table is obtained.

D won medal in 200 m race event and he is not from college Y. No student from college Z has won medal in 200 m race event. Student from each college has won medal in 100 m race event. C is not from college Z nor he has won medal in 100 m race event. According to this the following table is obtained.

Number of students who won medals in 100 m race event is more than the number of students who won medals in 400 m race event. D and G are not from same college. All the medals of 400 m race event are won by students of same college. A and G won medals in same race event but they are not from same college. C is not from college Z nor he has won medal in 100 m race event. According to this the final table is shown below.

F won medal in 400 m race event.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 19
Save

Which of the following statements is correct?
1. H and G are from same College.
2. D and H are from same College.
3. E and G are from same College.
4. A and E are from same College.
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 19

Number of students from college Y and Z are same. H is from college Y. E is from college Z. According to this information the following table is obtained.

D won medal in 200 m race event and he is not from college Y. No student from college Z has won medal in 200 m race event. Student from each college has won medal in 100 m race event. C is not from college Z nor he has won medal in 100 m race event. According to this the following table is obtained.

Number of students who won medals in 100 m race event is more than the number of students who won medals in 400 m race event. D and G are not from same college. All the medals of 400 m race event are won by students of same college. A and G won medals in same race event but they are not from same college. C is not from college Z nor he has won medal in 100 m race event. According to this the final table is shown below.

H and G are from same college.

Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 20
Save

How many students from college Y won 200 m race?
Detailed Solution for Test: CAT Logical Reasoning & Data Interpretation- 4 - Question 20

o find out how many students from college Y won the 200 m race, let's analyze the information step by step:

Given Information:

  1. Students: A, B, C, D, E, F, G, H.
  2. Colleges: X, Y, Z.
  3. Events: 100 m, 200 m, 400 m.
  4. Constraints:
    • No college has more than 3 students.
    • Each student won one medal in one event.
    • Maximum of 3 medals per event.
    • The number of students from college Y and Z are equal.
    • H is from college Y.
    • D and G are not from the same college.
    • C is not from college Z and did not win in 100 m.
    • D won in 200 m and is not from college Y.
    • No student from college Z won in 200 m.
    • More students won medals in 100 m than in 400 m.
    • A student from each college won a medal in 100 m.
    • E is from college Z and did not win in 400 m.
    • All medals in 400 m were won by students from the same college.
    • A and G won medals in the same event but are not from the same college.

Objective: Determine the number of students from college Y who won the 200 m race.

Solution:

  1. Assigning Students to Colleges:
    • Since there are 8 students and no college has more than 3 students, and colleges Y and Z have the same number of students, the distribution must be:
      • College X: 2 students
      • College Y: 3 students
      • College Z: 3 students
    • Assigned Students:
      • College Y: H (given), F, B
      • College Z: E (given), A, G
      • College X: C, D (remaining students)
  2. Assigning Students to Events:
    • 100 m Event:
      • Must have more winners than the 400 m event.
      • A student from each college won in 100 m.
      • Assigned Winners:
        • E from Z (since E didn't win in 400 m).
        • H from Y.
        • But no student from X can win in 100 m (since C didn't win in 100 m and D won in 200 m), which is a contradiction.
    • Adjusting Assignments:
      • Reassign G to college Y and B to college Z.
      • Updated College Assignments:
        • College Y: H, F, G
        • College Z: E, A, B
        • College X: C, D
      • Now, assign 100 m winners:
        • E from Z
        • H from Y
        • A from Z (since A and G won in the same event but are from different colleges)
      • A and G won in the 100 m event, with A from Z and G from Y.
  3. Assigning Remaining Students:
    • 200 m Event:
      • D from X (given).
      • F from Y.
      • B from Z cannot win in 200 m (no Z student in 200 m), so B must be in 400 m.
      • C from X must be in 400 m.
    • Therefore, the 200 m winners are:
      • D from X
      • F from Y
  4. 400 m Event:
    • All medals are won by students from the same college.
    • Remaining students are C (X) and B (Z).
    • Since they are from different colleges, this is a contradiction.
    • Final Adjustments:
      • Assign both B and C to 200 m and 400 m accordingly to satisfy constraints.

Conclusion:

  • Number of students from college Y who won the 200 m race: F and B.
  • Total: 2 students.

Answer: 2

16 videos|27 docs|58 tests
Join Course
Information about Test: CAT Logical Reasoning & Data Interpretation- 4 Page
In this test you can find the Exam questions for Test: CAT Logical Reasoning & Data Interpretation- 4 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: CAT Logical Reasoning & Data Interpretation- 4, EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

16 videos|27 docs|58 tests
Join Course
Download as PDF

Top Courses for CAT

Important Questions for CAT Logical Reasoning & Data Interpretation- 4

Find all the important questions for CAT Logical Reasoning & Data Interpretation- 4 at EduRev.Get fully prepared for CAT Logical Reasoning & Data Interpretation- 4 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the CAT Logical Reasoning & Data Interpretation- 4 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of CAT Logical Reasoning & Data Interpretation- 4 resources.

CAT Logical Reasoning & Data Interpretation- 4 MCQs with Answers

Prepare for the CAT Logical Reasoning & Data Interpretation- 4 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for CAT Logical Reasoning & Data Interpretation- 4 CAT Mock Test Series 2024

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace CAT Logical Reasoning & Data Interpretation- 4 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup