Test: CAT Logical Reasoning & Data Interpretation- 5 - CAT MCQ
20 Questions MCQ Test - Test: CAT Logical Reasoning & Data Interpretation- 5
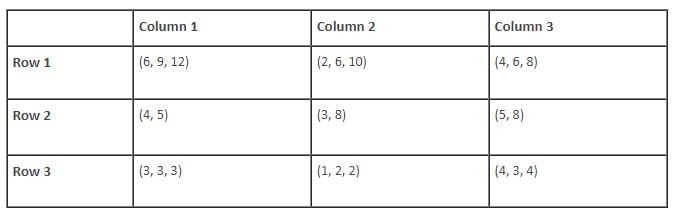
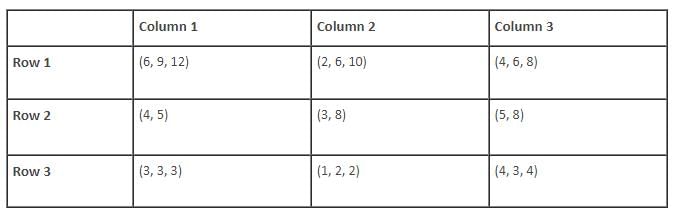
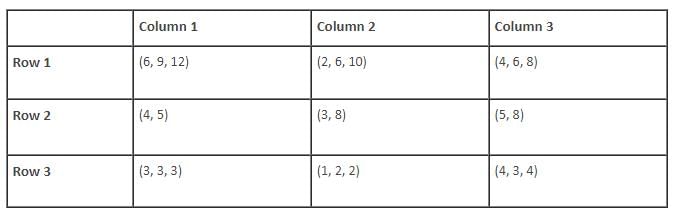
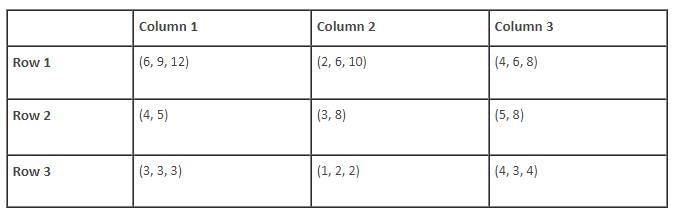
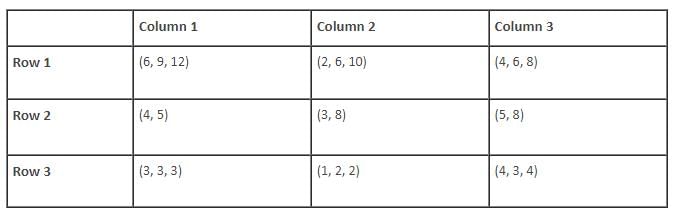
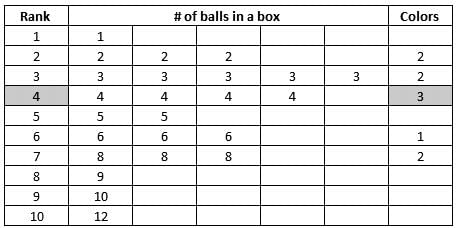
Find the total number of balls kept in the first row of column 3 and the third row of column 2.
Find the ratio of the total number of green balls to the total number of black balls.
Find the total number of slots for which the total number of balls in its boxes strictly exceeds 15.
Find the number of slots for which the total number of balls in its boxes is more than 10 and less than 20.
If all boxes are ranked in ascending order of their contents (balls), then which rank would be shared by boxes having maximum number of differently coloured balls?
If Wesley So and Richard Rapport lose in the second round, while Ian Nepomniachtchi and Anish Giri make it to the semifinals, then who will play with Magnus Carlsen in the quarterfinals, in the event Magnus Carlsen reaches the quarterfinals?
If the top eight rated players make it to the quarterfinals, then who amongst the players listed below will definitely not play against Magnus Carlsen in the final, in case Carlsen reaches the final?
If there are no upsets (a lower seeded player beating a higher seeded player) in the first round, and only match no. 6, 7 and 8 of the second round result in upsets, then who would meet Liren Ding in the quarterfinals, in case Liren Ding reaches the quarterfinals?
If in the first round, all even numbered matches (and none of the odd numbered ones) result in upsets, and there are no upsets in the second round, then who could be the lowest seeded player facing Magnus Carlsen in the semifinals?
What is the total number of matches played in the tournament?
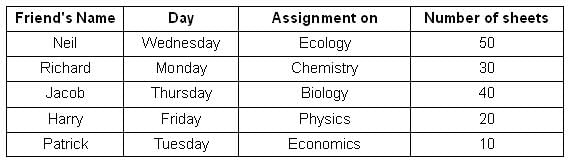
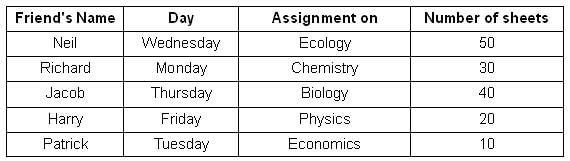
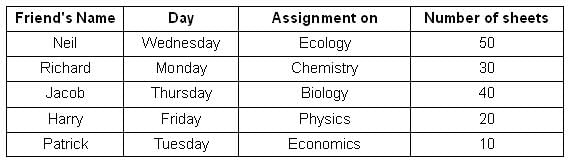
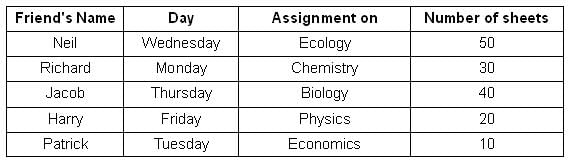
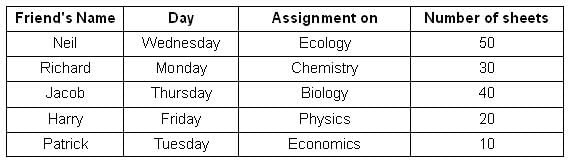
Who among the following went to the shop on Tuesday?
How many sheets were printed by the friend who made an assignment on Ecology?
The friend who took a copy of the least number of sheets went to the shop on
Which of the following statements is TRUE?
The difference between the average daily number of sheets printed in the first three days of the week and the last two days of the week is _____. Key in the value.
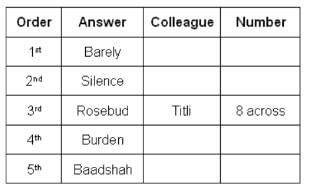
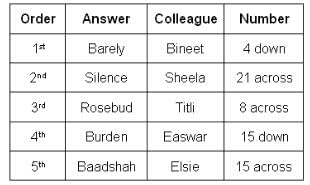
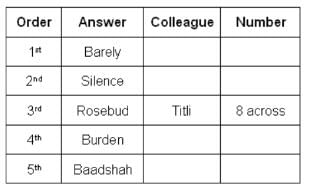
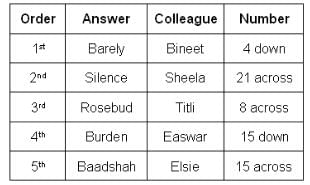
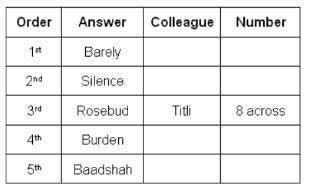
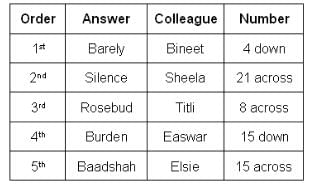
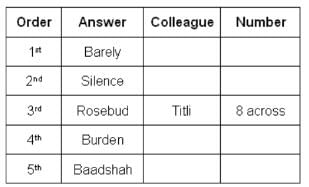
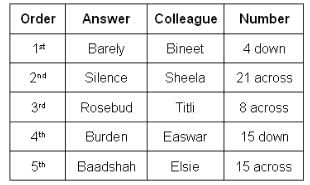
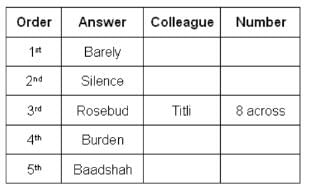
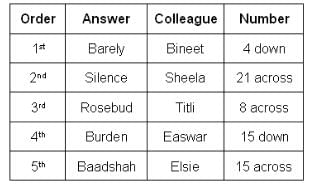
What could be Titli's answer?
Who produced the answer 'Burden'?