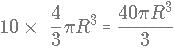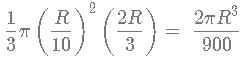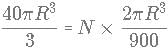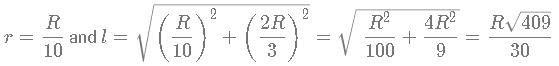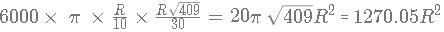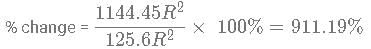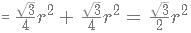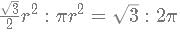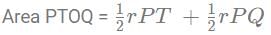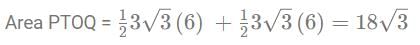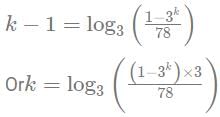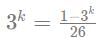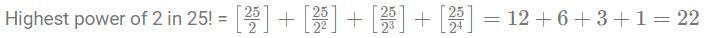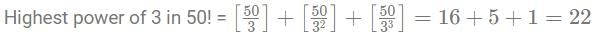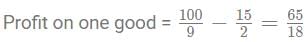Test: CAT Quantitative Aptitude- 3 - CAT MCQ
22 Questions MCQ Test Quantitative Aptitude (Quant) - Test: CAT Quantitative Aptitude- 3
The average age of a group of travellers is 25 years. For a certain trip to Australia, the average age has to be a maximum of 24 years, so they included A in their group to satisfy the criteria. For a certain trip to South Africa, the average age of the group has to be a minimum of 26 years. To satisfy this, the original group (excluding A) included B in their group. What is the average of the highest possible age of A and the lowest possible age of B?
A bag contains Rs. 1, 50 p and 25 p coins. The number of 25 p coins is numerically equal to the total value of all the 50 p coins (in Rs). Aso, the total amount in the bag is equivalent to one thousand 25 p coins. The number of Rs. 1 coins is 14 less than the total value of all 25 p coins(in Rs). What is the total value of all the 50 p coins as a percentage of the total amount of money present in that bag?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In Cracku, 60% of the enrolled students read newspaper A, 50% of the enrolled students read newspaper B, 30% of the enrolled students read newspaper C, 40% of the enrolled students read newspaper D. While a particular student may read more than one newspaper, each student must read at least one newspaper. It is known that no one reads 2 or 3 newspapers, which of the following is a possible number of enrolled students in Cracku?
A function f(x) is defined as 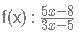
fn (x) is defined as f(f(...n times f(x))))
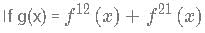
What is value of [g(12)]. [x] represents the greatest integer less than or equal to x
If a polynomial function exists such that 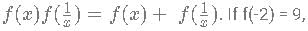 what is the absolute value of f(4)?
what is the absolute value of f(4)?
Let p be sum of all the values of k which satisfy the equation:
5{k}+2 = 2[k-1]
What is the value of [2p-1]?
Here {x} denotes the fractional part of x and [x] denotes the greatest integer less than or equal to x
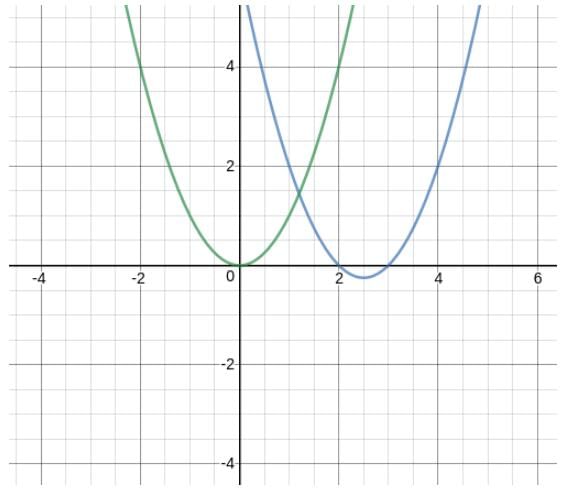
Find the minimum value of the following function:
f(x) = max (x2 - 5x + 6,x2)
10 spheres of radius "R" are melted into making right cones of radius 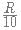 and height
and height 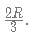 What is approximate change in the curved surface area?
What is approximate change in the curved surface area?
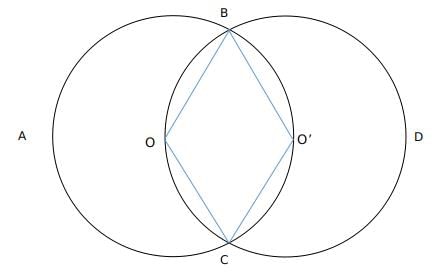
2 circles of the same radius are on a 2-D plane that exists such that the centre of one circle lies on the circumference of another circle. A quadrilateral is constructed by taking the two points of intersection of the circles and their centres. What is the ratio of the area of the quadrilateral to the area of 1 circle?
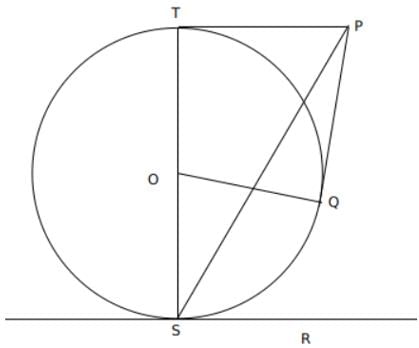
In the above figure, PT and RS are 2 parallel lines which are tangents to the circle with centre O. PQ is also a tangent to the circle
∠ PSO = 30º and PT = 6 units. What is the value of the area of PTOQ?
How many positive integral pairs (x, y) exists such that 4 < ∣x − 5∣ × ∣y − 7∣ < 7
How many non-zero integer values of x satisfy the equation given below such that x <= 10.
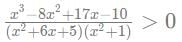
Cost of 1 pen, 3 pencils and 5 markers is Rs 100. Cost of 18 pencils, 2markers and 6 pens is Rs 320. What is the minimum possible cost of 1 marker, 1 pen and 1 pencils if it is given that the cost of each of the items is a natural number?
If t satisfies the following equation:
log3 78 + t − 6 = log3 (1 − 3t−5)
What is the value of |t|
An entrepreneur borrows an amount of Rs 20 lakhs from a local bank for a duration of 3 years at a 20% interest rate, compounded annually. At the end of each of these 3 years, he returns a certain amount of money to the bank. The amount returned at the end of each of these 3 years is the same. At the end of 3 years, the bank additionally demanded a cheque of Rs. 1.8 lakhs to settle the loan. What was the amount he used to pay at the end of each year?
A milk merchant buys milk at Rs 50 per litre, but while selling, he marks up the price by 20% and also mixes water to the milk such that the milk-water mixture he sells has 80% milk and 20% water. Assuming that the water has zero cost price, what discount percentage should he give to the mixture such that by selling it, he earns a 10% profit?
Ram was asked to calculate the sum of an arithmetic progression whose first term was 2 and common difference was 7. The total number of terms was 30. He wrote down all the 30 terms in ascending order and then started adding from smallest number. After calculating the sum of first x terms correctly, Ram started taking common difference as 14 instead of 7 and ended up with sum of 3210. How many factors does x − 4 has?
What is the number of common terms between the following series
A1: 4,10,16,22,28,..........,610
A2 : 2,9,16,23,............... 632
X = Highest power of 144 in 25!
Y = Highest power of 96 in 50!
How many of the following sentences are correct about the value Y - X?
1. It is a perfect square
2. It is a perfect cube
3. It is prime
4. It is even
A merchant purchases goods at the rate of 14 for Rs 105, marks them at the rate of 7 for Rs 140. If he offers 2 successive discounts on the marked price, d1% and d2%, such that d1 is one-fifth the markup percentage and d2 is half that of the value of d1, what is the profit/loss made by selling 90 goods?
Amar drives his car for 2 hours at a speed of 70 km/h, for 3 hours at a speed of 80 km/h and for 1 hour at a speed of 40 km/h and reaches his hometown. What is his average speed (in km/h)?
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|


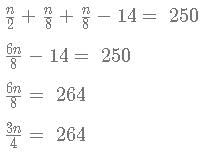

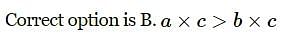
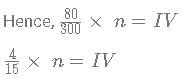
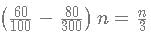
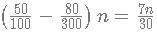
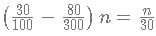
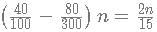
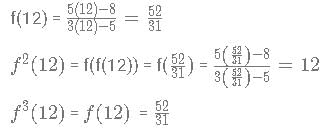
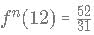
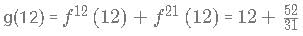
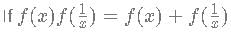 then f(x) has to be of form
then f(x) has to be of form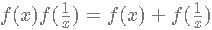 this can be written as
this can be written as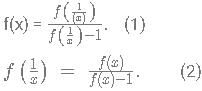
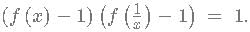
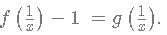
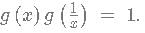

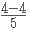 0. Thus k ={k}+[k] = 2.0
0. Thus k ={k}+[k] = 2.0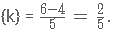 Thus k ={k}+[k] =
Thus k ={k}+[k] = 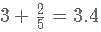
 Thus k ={k}+[k] =
Thus k ={k}+[k] = 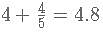
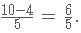 Which is not possible
Which is not possible