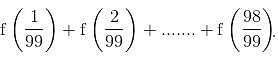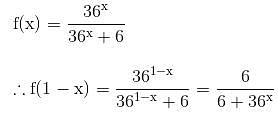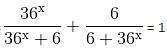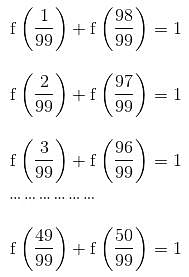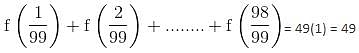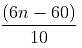Test: CAT Quantitative Aptitude- 5 - CAT MCQ
22 Questions MCQ Test Quantitative Aptitude (Quant) - Test: CAT Quantitative Aptitude- 5
If the interest compounded annually on a certain sum at a certain rate of interest for 2 years is equal to 40% of the simple interest on the same amount at same interest rate for thrice the time period, find the rate percentage.
Jagan, the video dealer, lends at most 10 DVDs at the cost of Rs. 300 per day and 12 CDs at the cost of Rs. 200 per day. Direct costs are Rs. 50 per day for DVDs and Rs. 30 per day for CDs. Also because some of the customers mishandled the products he had to spend Rs. 5000 on maintenance. In the month of March due to exams DVDs and CDs lending rate was 30% and 40% respectively, which kept on increasing gradually by 5% and 8% every month (i.e. rate became 35% and 48% respectively the next month). What is the profit for the month of May if his fixed monthly cost is Rs. 40,000?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A group of 10 students started playing pass-the-bucket. They stood in a row and the 1st student passed a bucket with 10 litres of milk. While passing it to the 2nd student in the row he spilled 5/3 litres. The 2nd student compensated for the lost volume by adding same amount of water and spilled 5/3 litres while passing the bucket to the 3rd student. This continued till the bucket was passed to the 10th student who replaced the volume of the spilled solution with an equal volume of water. What was the percentage of milk in the bucket when it was in the hands of the 5th student just before he handed it over to the 6th student?
Robin has a silver ball and a platinum ball each of radii 4 cm. The worth of each ball is Rs. 50,000. The worth of silver doubles every 2 years, while that of platinum remains the same. At the end of 6 years, Robin sells the silver ball and invests the money in a new platinum ball. The worth of a platinum ball is directly proportional to its volume. How much should the radius (in cm) of the new platinum ball be?
Ten years ago, the Edwards had 8 members and the average of their ages then was 33 years. Four years later, Mrs. Edward died at the age of 64 years and William Edward was born. After three more years, Mr. Edward died, at the age of 72 years and Liz Edward was born. Find the present average age of the family (in years).
Samrat covers the total journey of 810 km to his village partly by train and then by bus. The train is 20% faster than the bus. If the train were to travel for the number of hours, which normally would be hours travelled by bus, and the bus were to travel the remaining distance, then the time for the journey would reduce by 24 minutes. The normal travelling hours of bus and train are in the ratio 3:2. What is the speed(in km/hr) of the bus?
What is the number of solutions of the equation
How many three digit numbers exist such that their value is decreased by 99% when their digits are reversed?
Given a cube, I pick three random points from among its vertices. Let N be the number of ways in which three points can be selected such that they form a right angled triangle. What is N?
A circle with centre O has radius 12 cm. AD is the diameter and AB is the tangent to the circle at point A.
If a, b and c are the sides of a triangle, then which of the following is true?
The difference in the areas of circumscribing and inscribing circles of the region bounded by the curves y = -|x| + 12 andy = |x| + 4 will be:
If we draw graphs of the following equations using standard conventions, for how many of the graphs will a line parallel to the y-axis intersect more than once?
i. xy = 4
ii. y = tan(x)
iii. x2 +y2 = 8
iv. x = y2
v. |x| + |y| = 2
People who like chocolate and ice-cream is 25% of people who like only chocolate. People who like ice-cream are 66.66% of people who don’t like chocolate. People who like only ice-cream is 90% of people who don’t like ice-cream. What is the ratio of people who like both to none?
A student has to attempt exactly 10 questions out of 15 in an exam ensuring that at least 3 out of the first 5 questions are attempted. In how many ways can the questions be selected?
A potter makes more than 120 but less than 300 pots and arranges them in rows, with each row consisting of the same number of pots, for drying. He finds that if he places 6 pots more per row, he can arrange the pots in 10 less rows. How many pots does the potter make? Key in the value.
The arithmetic mean of a set of 20 observations is X. When three of the twenty observations, 12, 19 and 74 are discarded, the mean of the new set remains unchanged. What is the arithmetic mean, X?
In a company three projects were assigned to all the members of a company. Following information is also known: 12 members were selected for the entire three projects.
The ratio for number of members selected for only project A : only project B : only project C is 3 : 4 : 5.
The ratio for number of members selected for project B and C only : project C and A only : project A and B only is 2 : 3 : 4.
Q. If the ratio of sum of number of members for only A, only B, only C to the sum of members for A and B only, B and C only, A and C only is 20/7 and the ratio of sum of number of members of A and B only, B and C only, A and C only to the members selected for all the three projects is 21/4, then find the number of members selected for only project C.
Group Question
Answer the following question based on the information given below.
A and B together can complete some work in 24 days. If A, B and C work together, they can complete the same work in 18 days. B and C both have the same efficiency.
Q. , B and C start working together from the very first day. If A works for 8 days, B works for 16 days and C works till the end of the given work, how many days are required to complete the given work?
|
196 videos|131 docs|110 tests
|
|
196 videos|131 docs|110 tests
|


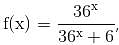 find the value of
find the value of