Test: CAT Quantitative Aptitude- 6 - CAT MCQ
22 Questions MCQ Test Quantitative Aptitude (Quant) - Test: CAT Quantitative Aptitude- 6
Sum of the first 11 and 12 terms of an A.P. is 420 and 555 respectively.
Fourth term of a G.P. (First term of the G.P. is 5) is equal to the 12th term of the A.P. What will be the common ratio of the G.P.?
Fourth term of a G.P. (First term of the G.P. is 5) is equal to the 12th term of the A.P. What will be the common ratio of the G.P.?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
f(x) = 13x
g(x) = |x|
h(x) = x2
What is the sum of all possible values of x for which hog(x) + fog(x) = 30?
g(x) = |x|
h(x) = x2
Find the number of four digit numbers such that the number formed by tens place and ones place in that order is equal to the sum of the digits at hundreds and thousands place.
Atul is standing at point P. P is 10 m away from a tree. Atul turns to his left and walks till point S. S is 5 m away from the tree. Baljit, who is facing the tree, also turns left from P through some angle and walks till point R. The angle traced by Baljit is twice of that by Atul. If R, S and the tree are along the same line, find the distance travelled by Baljit, if the distance between R and S is 3 m.
A is standing on the foremost point of a train moving at 270 km/hr in a straight line. He starts moving in the direction opposite to that of the train at 3 m/s. At the same time B standing on the rearmost part of the train starts moving in the direction of the train at 4 m/s. A person standing outside notices that when A moves 1800 m, B is 2100 m away from A. Find the length of the train.
Which of the following is the range of values of x?
1. -16 <x < 4
2. x > 6 orx < —16
3. 3 < x < 4
4. - 1 6 < x < 3 or 4 < x < 6
Type in the correct option number as your answer.
The integers 5417 and 5223 when divided by a two digit number N leave the same remainder. N = _______
A whole saler buys 100 watches from on estate at the rate of Rs.45.45 per watch and sells the mall in his own state for Rs 6817.5 He pays a certain percentage of the cost price as the tax. If he earns a total of 20% by selling the watches, then find the tax percentage levied over the purchased price.
What will be the remainder when 3136 is divided by 12 ?
A bank pays 4.5% compound interest per month for a principal amount P.
The amount becomes Pm in m months. Which of the following options best represent the graph between Pm (y-axis) and m (x-axis) will be:
Let g(x +1) g(x - 1) = g(x). then for what integral values of p would we have g(x+p) = g(x)?
Let, x and y be positive real numbers such that log2(x2 - y2) - log2(x + y) = 1 and log3x + log3y = 1. Then the value of y is
A petrol distributor adulterates petrol with kerosene and naphthalene. There are two containers of different capacities which contain this adulterated petrol. Container 1 contains 30% petrol and container 2 contains 45% petrol. If both these mixtures are mixed in a larger container in such a ratio that kerosene in it is 25% and naphthalene is 40%. Find the capacity of container 2(in litre) if the capacity of container 1 is 8 litres.
A square cuts the x m d y axes at (2, 0); (-2, 0) and (0, 2);(0, -2). I f the axes are rotated by 60° in anticlockwise direction, then find the ratio (smaller to larger) in which each side of the square will be divided into by any of the axes.
Oyo Cab service offers free ride to customers for a certain distance and then charges at a constant rate per kilometer. Biswas uses the cab to go to a nearby shopping complex and Amit goes to mall on the cab. The combined bill of Biswas and Amit amounts to Rs. 110. If the distance covered by Biswas on the cab had doubled, he would have paid Rs. 200 as charges to the cab driver, whereas in case of Amit, if the distance had doubled the charges would have been 50% less than the charges paid by Biswas in case of increased distance. What would be the amount paid by Biswas, if he travelled thrice the distance travelled by him initially?
The average age of a village X at the start of the year 2008 is 30 years. Every year starting from 2009, migrants - amounting to 20% of the population of village X in 2008 - move to village X. The average age at entry, for every batch of migrants is 5 years less than that of the village X at the start of 2008. Find the average age of the village X just after the third batch of migrants enter it.
Roshan has three daughters Riya, Piya and Siya. He divides 21 chocolates among them such that for every chocolate Riya receives, Siya receives 3 chocolates and for every chocolate that Piya receives, Riya receives 5 chocolates. How many chocolates did Siya get?
Find the sum of the digits in the expanded product 199,999,997 × 200,000,003.
In a computer network, there are 36 identical files to be distributed among 5 users. However, each user receives a number of files in multiples of three. How many ways are there to distribute the files under these conditions?
In a construction project, a group of N workers worked together to complete a building. They finished 70% of the construction in 20 days by working 8 hours a day. However, due to unforeseen circumstances, 15 workers had to leave the project. The remaining workers completed the remaining 30% of the construction in 10 days by working 12 hours a day. If the total work required for the project is considered one unit, key in the value of N?
Bus A left station S1 at 11 am for station S2. Another bus B having speed 75% of speed of A, left station S2 for station S1 at 12 pm. Two buses met each other at station S3, where the distance between S1 and S3 is 60% of that between S1 and S2. Find the time taken (in hours) by bus A for its journey from S1 to S2
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|




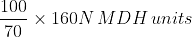
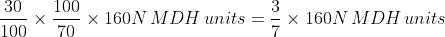
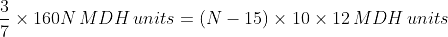

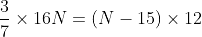
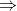
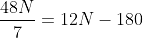
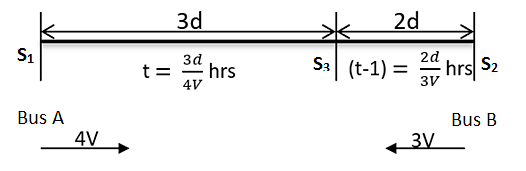
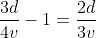
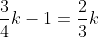
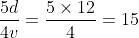 hours
hours














