Test: Coordinate Geometry- 1 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Coordinate Geometry- 1
Q.
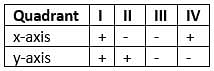
We divided the plane of the paper into four equal parts. by drawing two mutually perpendicular lines, X'OX and YOY'. These lines are called the axes. Here X'OX is called x-axis and YOY' is called y-axis. There axes divide the plane of the paper into four parts, called quadrants.
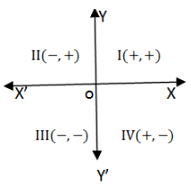
The position of a point in a plane is denoted by an ordered pair (a,b), where a is called the x co-ordinate and y is called y co-ordinate.
In which quadrant does the point(-4, -7) lie?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the distance of the point A(3, -3) from the origin.
P is a point on x-axis at a distance of 4 units from y-axis to its right. The co-ordinates of P are:
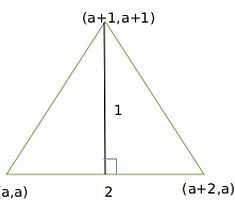
The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
A is a point on y-axis at a distance of 5 units from x-axis lying below x-axis. The co-ordinates of A are:
ABCD is a rhombus with the diagonals AC and BD intersection at the origin on the x-y plane. The equation of the straight line AD is x + y = 1. What is the equation of BC?
|
196 videos|131 docs|110 tests
|
|
196 videos|131 docs|110 tests
|