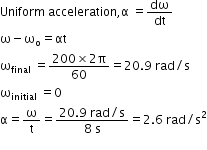Test: Kinematics of Rotational Motion - NEET MCQ
20 Questions MCQ Test Physics Class 11 - Test: Kinematics of Rotational Motion
Direction of linear velocity of a particle rotating in a circular motion is :
A ball is under the effect of circular motion about a perpendicular axis with respect to the reference direction. The angular position (in radians) is given by the following function θ = t2 - 0.4t + 2 .The angular position when angular velocity is zero is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let  H and
H and  E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.
E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.
 H and
H and  E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.
E respectively be the angular speeds of the hour hand of a watch and that of the earth around its own axis. Compare the angular speeds of the earth and hour hand of a watch.The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 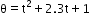 . The linear velocity of the particle
. The linear velocity of the particle
All the points of a rigid body rotating about the given axis have same :
A mixer grinder rotates clockwise, its angular velocity will be :
Which of the following is not a unit of angular displacement?
In an equilateral triangle of length 6 cm , three masses m1= 40g , m2= 60g and m3= 60g are located at the vertices. The moment of inertia of the system about an axis along the altitude of the triangle passing through m1 is
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .
A boy is playing with a tire of radius 0.5m. He accelerates it from 5rpm to 25 rpm in 15 seconds. The linear acceleration of tire is
The angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycle per second. The momentum of inertia of the body about the axis of rotation is
A merry- go- round ( diameter 4.0 m ) starts from rest and uniformly accelerates until it rotates at 0.8 rev/min. This occurs in 11s. Once it has reached this rate , it rotates at 0.8 rev/min uniformly . Determine the angular acceleration
A demo CD, 8 cm in diameter, spins 200 rev/min. Determine its linear velocity in cm/s for a point 3 cm from the center.
A wheel rotates with a constant acceleration of 2.0 rad/s2 . If the wheel starts from rest, the number of revolutions it makes in the first ten seconds will be approximately:
The angular velocity of a second hand of a clock is :
A car is decelerating uniformly from velocity v1 to velocity v2 while getting displaced by s. If the diameter of the wheel is d, the angular acceleration of the wheel is
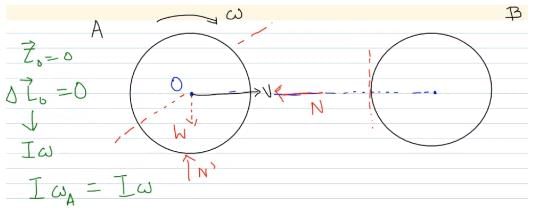
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and center of mass velocity v. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ωA and ωB respectively. Then
If n is the frequency of rotation of a body, its angular velocity is:
|
97 videos|378 docs|103 tests
|