Complex Numbers & Quadratic Equations- 2 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Complex Numbers & Quadratic Equations- 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The smallest positive integer n for which 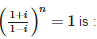
If the cube roots of unity are 1, ω,ω2, then roots of the equation (x−1)3+8 = 0 are :
The number of solutions of the equation Im (z2) = 0,|z| = 2 is
If z1 and z2 are non real complex numbers such that |z1| = |z2| and Arg(z1)+Arg(z2)= π, then z1 =
The complex numbers sinx + i cos2x and cosx – i sin2x are conjugate to each other, for
The value of (-1 + √-3)2 + (-1 - √-3)2 is
If α is a complex a number such that α2+α+1 = 0 then α31 is
The points z = x + iy which satisfy the equation | z | = 1 lie on
The points of the complex plane given by the condition arg. (z) = (2n + 1) π, n ∈ I lie on
If z = x + yi ; x ,y ∈ R, then locus of the equation , where c ∈ R and b ∈ C, b ≠ 0 are fixed, is
The complex number z which satisfies 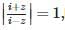 lies on
lies on
If ω is a cube root of unity, then the linear factors of x3+y3 in complex numbers are
If α,β are non-real cube roots of unity then αβ + α5+β5 equals
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|


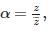 then |α| is equal to :
then |α| is equal to : 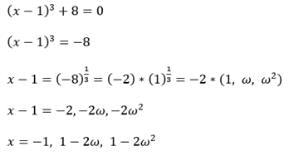
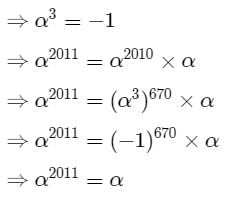
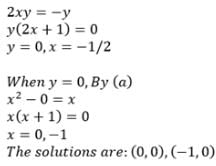

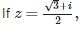 then z69 is equal to :
then z69 is equal to :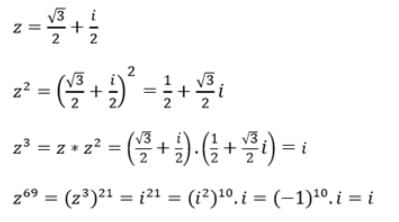
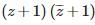 can be expressed as
can be expressed as














