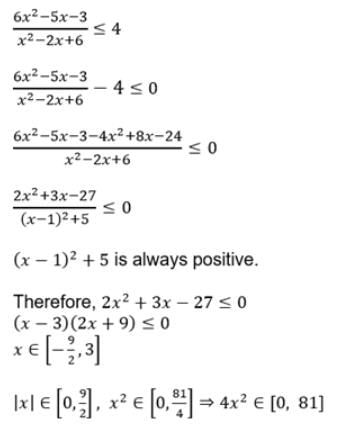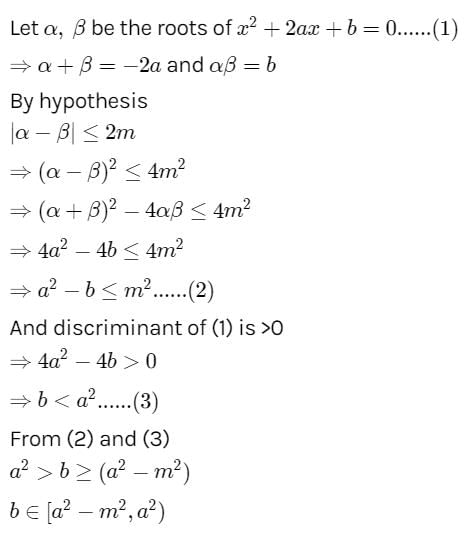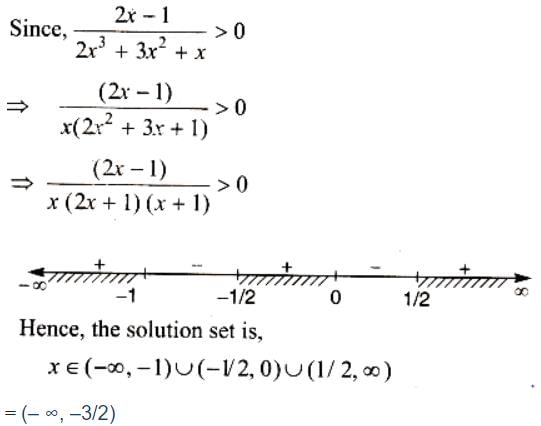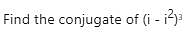Test: Complex Numbers - Commerce MCQ
29 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Complex Numbers
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the roots of the equation x2 - 5x + 16 = 0 are a, b and the roots of the equation x2 + px + q = 0 are (a2 + b2) and , then-
The number of the integer solutions of x2 + 9 < (x + 3)2 < 8x + 25 is
Let a > 0, b > 0 and c > 0. Then both the roots of the equation ax2 + bx + c = 0
The set of all solutions of the inequality < 1/4 contains the set
Consider y =, where x is real, then the range of expression y2 + y – 2 is
The values of k, for which the equation x2 + 2(k – 1) x + k + 5 = 0 possess atleast one positive root, are
If coefficients of the equation ax2 + bx + c = 0, a < 0 are real and roots of the equation are non–real complex and a + c + b < 0, then
If the roots of the equation x2 + 2ax + b = 0 are real and distinct and they differ by at most 2m, then b lies in the interval
If the roots of the quadratic equation x2 + px + q = 0 are tan 30º and tan 15º respectively, then the value of 2 + q – p is
If (1 – p) is root of quadratic equation x2 + px + (1 – p) = 0, then its roots are
The values of x and y besides y can satisfy the equation (x, y ∈ real numbers) x2– xy + y2 – 4x – 4y + 16 = 0
For what value of a and b the equation x4 – 4x3 + ax2 + bx + 1 = 0 has four real positive roots ?
If a, b are roots of the equation ax2 + bx + c = 0, then the value of a3 + b3 is
If a, b are roots of the equation ax2 + bx + c = 0 then the equation whose roots are 2a + 3b and 3a + 2b is
If S is the set of all real x such that is positive, then S contains
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|