Test: Complex Numbers & Quadratic Equations - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Complex Numbers & Quadratic Equations
The complex numbers z = x + iy which satisfy the equation 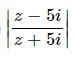 = 1 lie on
= 1 lie on
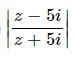 = 1 lie on
= 1 lie onThe inequality | z − 4 | < | z −2 | represents the region given by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If (√3 + i)10 = a + ib: a, b ∈ R, then a and b are respectively :
Let x,y ∈ R, hen x + iy is a non real complex number if
Let x,y ∈ R, then x + iy is a purely imaginary number if
Multiplicative inverse of the non zero complex number x + iy (x,y ∈ R,)
The locus of z which satisfied the inequality log0.3|z –1| > log0.3|z – i| is given by
The inequality | z − 6 | < | z − 2 | represents the region given by
Distance of the representative of the number 1 + I from the origin (in Argand’s diagram) is
If ω is a cube root of unity , then (1+ω)(1+ω2)(1+ω4)(1+ω8)...... upto 2n factors is
If points corresponding to the complex numbers z1, z2, z3 and z4 are the vertices of a rhombus, taken in order, then for a non-zero real number k
If k , l, m , n are four consecutive integers, then  is equal to :
is equal to :
i2+i4+i6+........... up to 2k + 1 terms, for all k belongs to natural numbers N.
If i2=−1, then sum i+i2+i3+....... to 1000 terms is equal to
If |z1| = 4, |z2| = 4, then |z1 + z2 + 3 + 4i| is less than
If If ω is a non real cube root of unity and (1+ω)9 = a+bω;a,b ∈ R, then a and b are respectively the numbers :
In z = a + bι, if i is replaced by −ι, then another complex number obtained is said to b
If (x + iy) (3 - 4i) = (5 + 12i), then 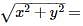
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|


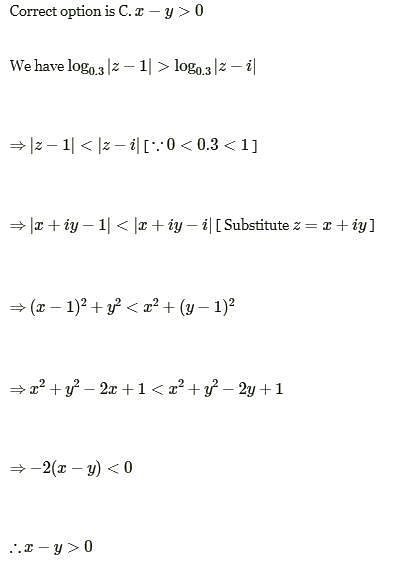 =
=

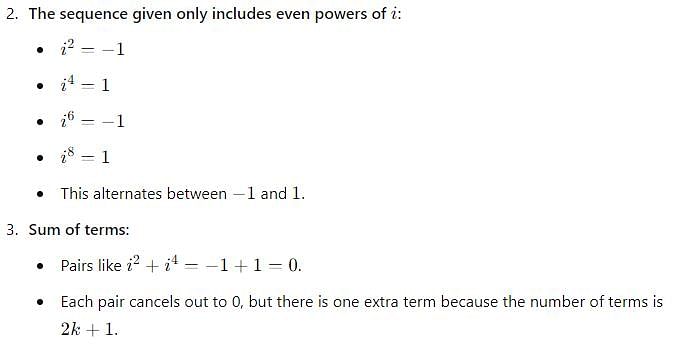
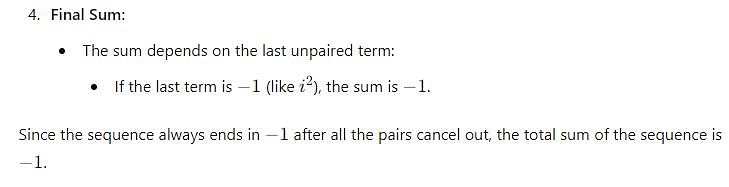

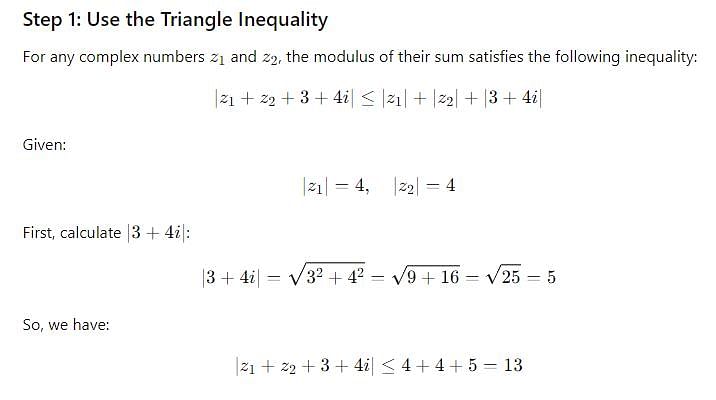

 z ≠ -1 is
z ≠ -1 is = 2n α, then α is equal to :
= 2n α, then α is equal to :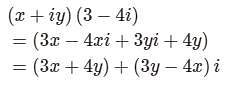

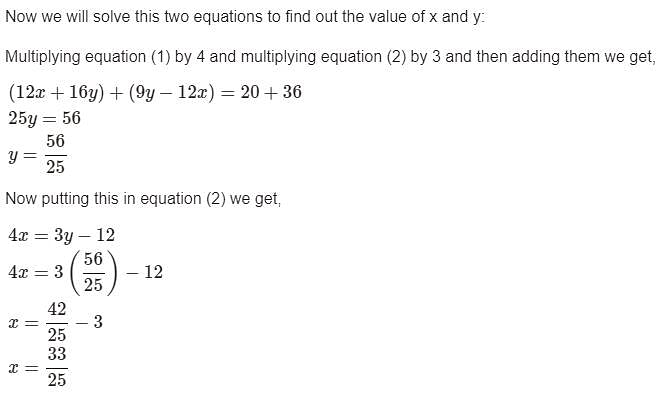


 This is Equation of a Circle.
This is Equation of a Circle.














