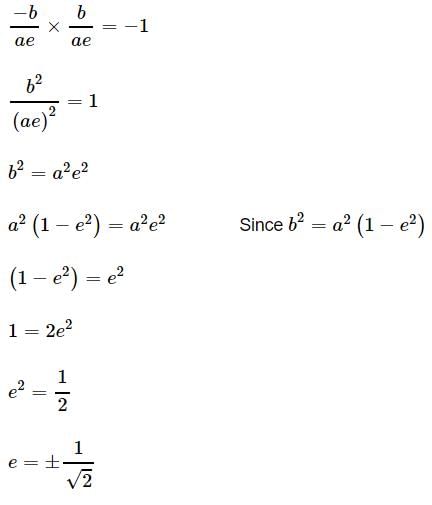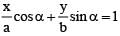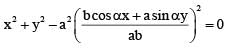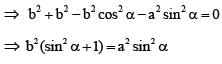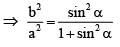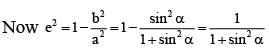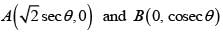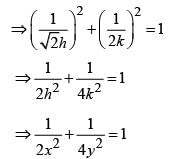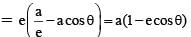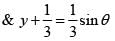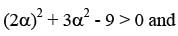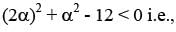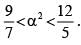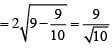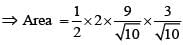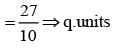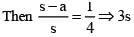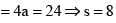Test: Ellipse- 3 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Ellipse- 3
An ellipse having foci at (3,3) and (-4,4) and passing though the origin has eccentricity equal to
The length of the major axis of the ellipse (5x - 10)2 + (5y + 15)2 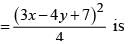
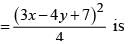
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The eccentric angle of a point on the ellipse 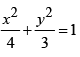 at a distance of 5/4 units from the focus on the positive x-axis, is
at a distance of 5/4 units from the focus on the positive x-axis, is
From any point P lying in first quadrant on the ellipse PN is drawn perpendicular to the major axis and produced at Q so that NQ equals to PS, where S is a focus. Then the locus of Q is
If a tangent of slope 2 of the ellipse is normal to the circle x2 + y2 + 4x + 1 = 0 , then the maximum value of ab is
An ellipse has the points (1, -1) and (2, -1) as its foci and x +y - 5 = 0 as one of its tangents. Then the point where this line touches the ellipse is
From point P (8, 27) , tangent PQ and PR are drawn to the ellipse Then the angle subtended by QR at origin is
An ellipse is sliding along the co-ordinate axes. If the foci of the ellipse are (1,1) and (3,3), then area of the director circle of the ellipse (in sq. units) is
The equation of the ellipse whose axes are coincident with the co-ordinates axes and which touches the straight lines 3x - 2y - 20 = 0 and x + 6y - 20 = 0 is
Number of point on the ellipse from which pair of perpendicular tangents are drawn to the ellipse
If maximum distance of any point on the ellipse x2 + 2y2 + 2xy = 1 from its centre be r, then r is equal to
The equation of the line passing through the centre and bisecting the chord 7x +y -1 = 0 of the ellipse
Eccentricity of ellipse such that the line joining the foci subtends a right angle only at two points on ellipse, is
The tangent at the point ‘a’ on the ellipse meets the auxiliary circle in two points which subtends a right angle at the centre, then the eccentricity ‘e’ of the ellipse is given by the equation :
The number of values of c such that the straight line y = 4x+ c touches the curve
If tangents are drawn to the ellipse x2 + 2y2 = 2, then the locus of the midpoint of the intercept made by the tangent between the coordinate axes is
An ellipse with major and minor axes, 6√3 and 6 respectively slides along the coordinate axes and always remains confined in the first quadrant. If the length of arc described by the centre of the ellipse is then the value of k is
Consider the ellipse and the parabola y2 = 2x. They intersect at P and Q in the first and fourth quadrants respectively. Tangents to the ellipse at P and Q intersect the x-axis at R and tangents to the parabola at P and Q intersect the x-axis at S. If the area of quadrilateral PQRS, is λ then
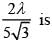
The area of the quadrilateral formed by the tangents at the end points of latus rectum of the ellipse 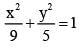 is k then k/9 is
is k then k/9 is
The length of the focal chord of the ellipse which is inclined to x – axis at an angle 45° is λ, then
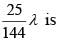
Q is a point on the auxiliary circle corresponding to the point P of the ellipse If T is the foot of the perpendicular dropped from the focus S on to the tangent to the auxiliary circle at Q then the ΔSPT is :
Let x and y satisfy the relation x2 + 9y2 - 4x + 6y + 4 = 0, then maximum value of the expression (4x - 9y),
A rectangle ABCD has area 200 square units. An ellipse with area 200π passes through A and C and has foci at B and D, then
A tangent to the ellipse at any point P meet the line x = 0 at a point Q. Let R be the image of Q in the line y = x, then circle whose extremities of a diameter are Q and R passes through a fixed point. The fixed point is
If the curve x2 + 3y2 = 9 subtends an obtuse angle at the point (2α, α), then a possible value of α2 is
Let S = 0 be the equation of reflection of about the line x – y – 2 = 0. Then the locus of point of intersection of perpendicular tangents of S is
Any ordinate MP of a ellipse meets the auxiliary circle in Q, then locus of point of intersection of normals at P and Q to the respective curves, is
The radius of the largest circle whose centre at (-3,0) and is inscribed in the ellipse 16x2 + 25y2 = 400 is
The line passing through the extremely A of the major axis and extremity B of the minor axis of the ellipse x2 + 9y2 = 9 meets its auxiliary circle at the point M . Then the area of the triangle with vertices at A,M and the origin O is
Coordinate of the vertices B and C of triangle ABC are respectively (2, 0) and (8, 0). The vertex ‘A’ is varying in such a way that Then the locus of ‘A’ is an ellipse whose major axis is of length.
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|



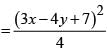
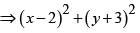
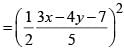

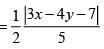
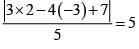
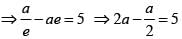
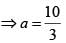
 be the tangent
be the tangent
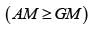
 ......(i)
......(i)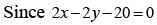
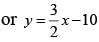
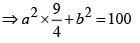
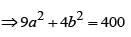 ......(ii)
......(ii)