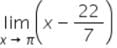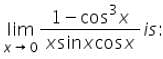Courses
Get the App Signup / Login

Test: Introduction And Algebra Of Limits


10 Questions MCQ Test Mathematics (Maths) Class 11 | Test: Introduction And Algebra Of Limits


Description
This mock test of Test: Introduction And Algebra Of Limits for JEE helps you for every JEE entrance exam. This contains 10 Multiple Choice Questions for JEE Test: Introduction And Algebra Of Limits (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Introduction And Algebra Of Limits quiz give you a good mix of easy questions and tough questions. JEE students definitely take this Test: Introduction And Algebra Of Limits exercise for a better result in the exam. You can find other Test: Introduction And Algebra Of Limits extra questions, long questions & short questions for JEE on EduRev as well by searching above.
QUESTION: 1

If the right and left hand limits coincide, we call that common value as the limit of f(x) at x = a and denote it by

Solution:

If the right-hand and left-hand limits coincide, we say the common value as the limit of f(x) at x = a and denote it by limx→a f(x) = l

  • If limx→a- f(x) is the expected value of f at x = a given the values of ‘f’ near x to the left of a. This value is known as the left-hand limit of ‘f’ at a.

  • If limx→a+ f(x) is the expected value of f at x = a given the values of ‘f’ near x to the right of a. This value is known as the right-hand limit of f(x) at a.

QUESTION: 2

If f(x) = 2, then 

Solution:

f(x) = 2
Hence it doesnt contain any variable
so, lim(x → 2) f(x) = 2

QUESTION: 3

Solution:

lim(x → π ) (x - 22/7)
Taking limit, we get 
⇒ π - 22/7

QUESTION: 4

For the limit of a function to exist we must have​
Solution:

Recall for a limit to exist, the left and right limits must exist (be finite) and be equal.

QUESTION: 5

Let f be any function, such that 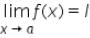 exists, then ​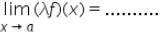
Solution:

lim(x → a) f(x) = l
λf(x) = λl 

QUESTION: 6

Let f(x) and g(x) be two function, such that 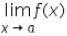 and 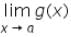 exists, then the limit of the product of the function f(x) and g(x) is given by
Solution:

By algebric property of limits,
Limit of products = product of limits
lim(x → a) (f(x)*g(x)) = lim(x → a) f(x) * lim(x → a) g(x)

QUESTION: 7

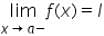 is the expected value of f at x = a given the values of f near x to the left of a. This value is called the……….of f at a.​
Solution:
QUESTION: 8

As x → a, f(x) → l, then l is called the……..of the function f(X) which is symbolically written as…….
Solution:

The number L is called the limit of function f(x) as x → a if and only if, for every ε>0 there exists δ>0
which is written as 
lim (x → a) |f(x) − l|
lim (x → a) f(x) = l

QUESTION: 9

The value of 
Solution:

QUESTION: 10

Consider the function f(x) = x + 10. Let us compute the value of the function f(x) for x very near to 5. Some of the points near and to the left of 5 and right to the 5 are given in the table.​
Solution:

Recommended Content

Recommended Tests

Related tests
Follow Us
© EduRev