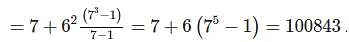Test: Permutation & Combination- 2 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Permutation & Combination- 2
MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Permutation and Combination under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
From a group of 7 men and 6 women, five persons are to be selected to form a committee so that at least 3 men are there on the committee. In how many ways can it be done?
In how many different ways can the letters of the word 'CORPORATION' be arranged so that the vowels always come together?
The sum of all the possible numbers of 4 digits formed by digits 3, 5, 5, and 6 using each digit once is
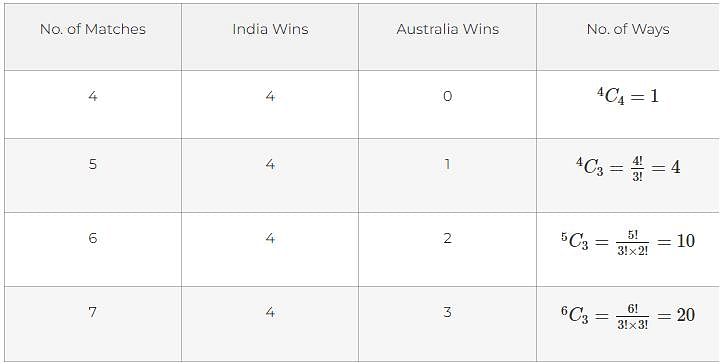
India and Australia player one-day international cricket series until anyone team win 4 matches. No match ended in a draw. In how many ways can the series be won?
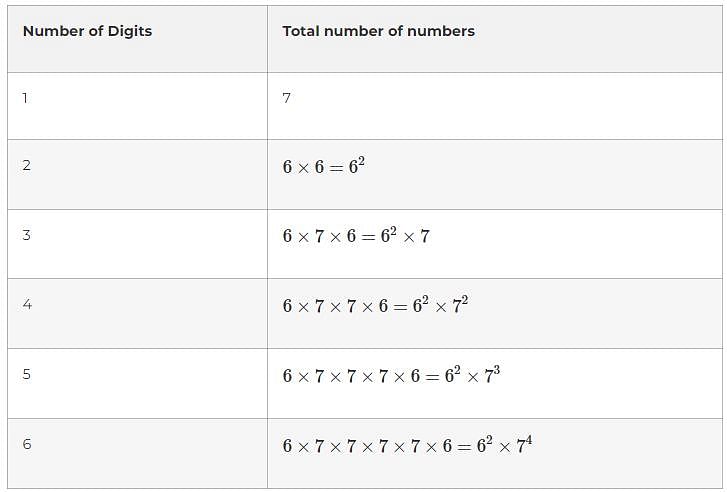
What is the number of whole numbers formed on the screen of a calculator which can be recognised as numbers with (unique) correct digits when they are read inverted? The greatest number that can be formed on the screen of the calculator is 999999.
The number of ways in which 4 squares can be chosen at random on a chess board such that they lie on a diagonal line?
There are 4 letters and 4 addressed envelopes. If each letter is randomly placed in an envelope, then in how many ways can wrong choices be made?
How many words can be formed with the letters of the word 'PATALIPUTRA' without changing the relative order of the vowels and consonants?
|
196 videos|131 docs|110 tests
|
|
196 videos|131 docs|110 tests
|