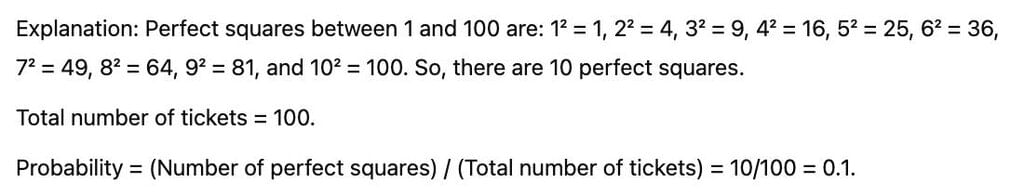Test: Applications of Probability - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - Test: Applications of Probability
Harry tosses two coins simultaneously. The probability of getting at least one head is
An urn contains lottery tickets numbered from 1 to 100. If a ticket is selected at random, then the probability that it is a perfect square is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the probability of winning a game is 0.3, the probability of losing it is
Three face cards of spade are removed from a well shuffled pack of 52 cards and a card is drawn from the remaining pack. The probability of getting a black face card is
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. The probability that it bears a two digit number is:
A card is drawn from a well-shuffled deck of 52 playing cards. The probability that the card will not be an ace card is
Three unbiased coins are tossed. What is the probability of getting at most two heads?
Two coins are tossed simultaneously once. Find the probability of getting at least one head and one tail.
A bag contains 3 white and 5 red balls. If a ball is drawn at random, the probability that the drawn ball is red is
The probability that a consonant is selected from the English alphabet is
Harmeet tosses two coins simultaneously. The probability of getting at least one head is
The probability of getting a number less than 5 in a single throw of dice is
All the three face cards of spade are removed from a well shuffled pack of 52 cards & card is drawn from the remaining pack. Find the probability of getting a black face card.
A fair die is cast in the game of ‘Ludo’. The probability of getting a score greater than 6 is
Aarti selects a card from a pack of well shuffled 52 playing cards. She needs an ace to win the game. The probability of Aarti losing the game is
In a throw of a die, the probability of getting a prime number is
One card is drawn from a deck of 52 cards. The probability of drawing a black card is
A bag has 9 red, 7 green and 4 blue balls. A student randomly selects a ball from the bag. The probability of not getting a blue ball is
What is the probability of getting a king when a card is drawn from a well shuffled deck of 52 playing cards?
Cards each marked with one of the numbers 4, 5, 6 …20 are put in a box and mixed thoroughly. One card is drawn at random from the box. The probability of getting an even prime number is
A die is thrown once. Find the probability of getting a number that is either composite or prime.
Out of a day’s production, which is 1000 machine parts, 100 were found to be sub-standard. The probability that a part selected at random being up to the standard is
From a well-shuffled pack of 52 cards, a card is drawn at random. The probability that it is a face card is:
One card is drawn from a deck of 52 cards. The probability of drawing a black card is
The probability that a leap year has 53 Sundays is
|
126 videos|457 docs|75 tests
|
|
126 videos|457 docs|75 tests
|