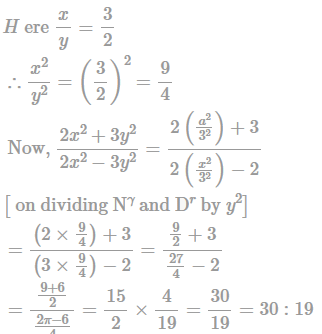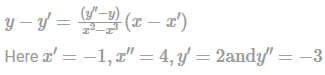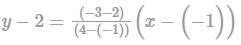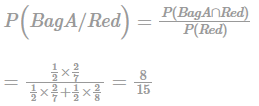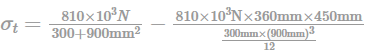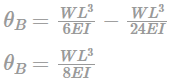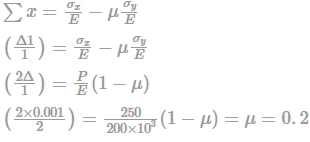Practice Test: Civil Engineering (CE)- 12
65 Questions MCQ Test GATE Civil Engineering (CE) 2023 Mock Test Series | Practice Test: Civil Engineering (CE)- 12
| 1 Crore+ students have signed up on EduRev. Have you? |
In the following question, four words are given out of which one word is incorrectly spelt. Select the incorrectly spelt word
Flounder=> suffer mentally
Anoint=> Nominate or choose (someone) as successor to or leading candidate for a position
Maneuver=> Move, ploy, manipulate
The smallest angle of a triangle is equal to two thirds of the smallest angle of a quadrilateral. The ratio between the angles of the quadrilateral is 3: 4: 5: 6. The largest angle of the triangle is twice its smallest angle. What is the sum, in degrees, of the second largest angle of the triangle and the largest angle of the quadrilateral?
So, 3x + 4x + 5x + 6x = 360
x = 20
Smallest angle of quadrilateral = 3 × 20 = 60 °
Smallest angle of triangle = 2/3 ×60∘ = 40∘
Largest angle of triangle = 2 × 40 ° = 60 °
Three angles of triangle are 40 °, 60 °, 80 °
Largest angle of quadrilateral is 120 °
Sum (2nd largest angle of triangle + largest angle of quadrilateral)
= 60 ° + 120 ° = 180 °.
If x : y = 3 : 2, then the ratio 2x2 + 3y2 : 3x2 - 2y2 is equal to
In the following question, out of the five alternatives, select the word similar in meaning to the given word/phrase.
Thinking too much about something
Somnambulism = the habit of walking in one's sleep.
Obsession = something or someone that you think about all the time.
Hallucination = a sensory experience of something that does not exist outside the mind.
Soliloquy = an act of speaking one's thoughts aloud when by oneself or regardless of any hearers, especially by a character in a play.
So, the correct word is "obsession".
In the following question, out of the four alternatives, select the word opposite in meaning to the given word.
Adipose
corpulent = fat, obese
glutinous = viscose, sticky
oleaginous = resembling or having the properties of oil
Select the related word/letters/number from the given alternatives.
Psychology : Mind :: Arithmetic : ?
This problem is based on the subject and its area of study.
Psychology is the science or study of the mind. Arithmetic is the branch of Mathematics that deals with computing of numbers (Addition, Subtraction, Multiplication and Division).
Hence, option B is the right answer.
Select the most appropriate option to fill in the blank.
As he could not execute the work properly, he had no option _____ to leave the organization.
"No option" is generally followed by the conjunction "but". Therefore, option D is the correct answer. See some examples
I had no option but to open the gate.
She has no option but to quit her studies.
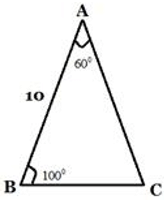
In a triangle ABC, angle A = 60o , angle B = 100o and AB = 10cm. find AC.
By angle sum property angle C= 20 degree
as we know from sin formula
SinA/BC= SinB/AC= SinC/AB
Sin 100°/ AC= Sin 20°/ 10
What is the equation of the line which passes through the points (-1,2) and (4,-3)?
Equation of a line passing through two given paints is given by
Therefore, equation of the line passing through these two paints is
⇒ y−2 = −1(x+1)
⇒ x + y = 1
P and Q can do a project in 25 and 50 days respectively. In how many days can they complete 18% of the project if they work together?
According to the question
P and Q can do a project in 25 and 50 days respectively.
Let us assume total unit of work available is 50 (LCM of 25 & 50)
And, P does 2 unit of work daily to get it completed in 25 days
Likewise, Q does 1 unit of work daily.
Therefore, total work done by them in 1 day=3 unit
Now, no. of days requires to complete 18% of the project if they work together
⇒ 18% of 50) / 3
⇒ 9/3=3 days
Hence the correct answer is option B
If the median of (x-1), (x-1), (x-4), (x+4), (x-3) is zero then the value of x is ________?
I.e. x-4, x-3, x-1, x+1, x+4
Now x-1 = 0
X = 1
A box contains 2 identical bags A and B . Bag A contains 2 Red and 5 Green balls. Bag B contains 2 Red and 6 Green Balls. A person draws a ball at random. If the drawn ball was Red what is the probability that it was from bag A?
If 2x - 3y = 24 and 3x + 4y = 2, find the value of x - y?
2x−3y = 24−−x−x−z−(1)
3x+4y = 2−x−z−z−(2)
If we multiply (1) by 4 and (2) by 3, we get 8x−12y = 96−−x−y−(3)
9x+12y = 6−x−−(4)
Now adding equation (3) and (4), we get 17x = 102
x = 102÷17
x = 6
On substituting x=6 in (1), we get y as:
12−3y = 24
−3y = 12
y = −4
Since values of x and y are known, so finding value of x−y will result in:
x−y = 6−(−4) = 6+4 = 10
x−y = 10, so correct option is ©
If A and B are invertible matrices, then inverse of AB is:
= (A1)A-1 = AA-1 = 1
Also, (B-1 A‑1) (AB) = 1
(AB)-1 = B-1 A-1
A 400g/L solution of common salt was discharged into a stream at a constant rate of 45l/s. At a d/s section where salt solution is known to have completely mixed with the stream flow equilibrium concentration was read as 100 ppm. If a background concentration of 18ppm is applicable, then, the discharge in the stream in m3/s is ___________.
Qt = 45I/s=0.045m3/s
C1 = 0.4
C2 = 0.0001
C0 = 0.000018
∴ Q = 0.045(0.4−0.0001)/0.0001−0.000018 = 219.45m3/s
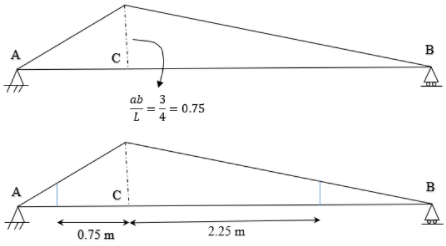
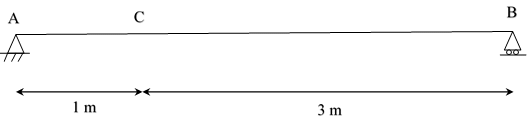
Find the maximum bending moment occuring at the point C due to a moving uniform load of 2 kN/m having a length of 3 m.
Maximum bending moment occurs at C when it divides the load in the same ratio as it divides the span, i.e. 1: 3 So total bending moment, area of ILD multiplied with load
[1/2 × (0.1875 + 0.75) × 0.75 + 1/2 × (0.1875 + 0.75) × 2.25] × 2
= [12 × (0.1875+0.75)×3] × 2 = 2.8125kNm
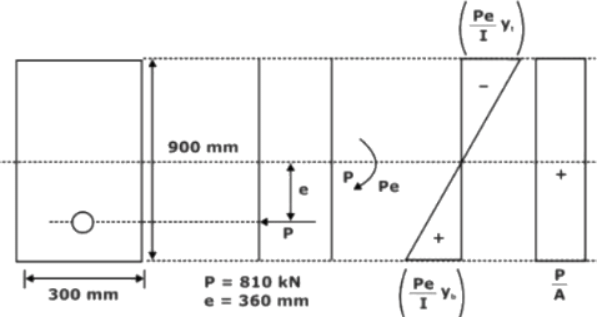
A prestressed concrete beam of size 300 mm × 900 mm is prestressed with an initial prestressing force of 810 kN at an eccentricity of 360 mm at mid-span. Stress at the top fibre due prestress alone
= 3MPa − 7.2MPa
= −4.2N/mm2
For two cycles coupled in series, the topping cycle has an efficiency of 40% and the bottoming cycle has an efficiency of 30%. The overall combined cycle efficiency is:
η = 0.40 + 0.30 − 0.4 × 0.3
η = 58%
Hence, the correct answer is 58%.
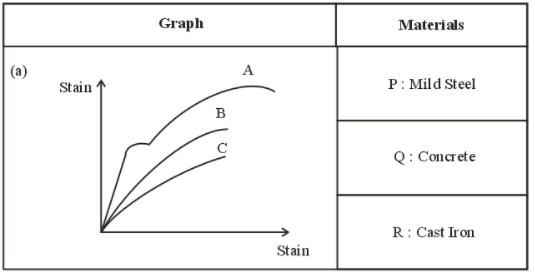
Which of the following statements is incorrect?
A horizontal jet of water with its cross–sectional area of 0.0028 m2 hits a fixed vertical plate with a velocity of 5 m/s. After impact the jet splits symmetrically in a plane parallel to the plane of the plate. The force of impact (in N) of the jet on the plate is
the velocity in x direction becomes zero after impact so using impulse momentum theorem
F = ρ0Q1V1 − ρωQ2V2 = ρωQ(V1−0)
Q = AV = 0.0028 × 5 = 0.014 ρω = 1000kg/m3
So ForceF = 1000 × 0.014 × (5−0)
= 70N
Read the following statements:
i. The minimum spacing required for the longitudinal reinforcement increases as the grade of steel increases.
ii. Less strain is required due to the high grade of steel.
Which of the above statements are incorrect?
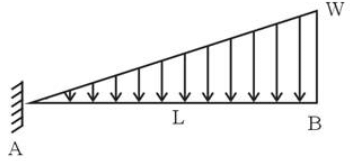
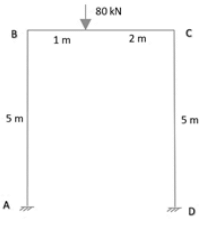
A portal frame is loaded as shown. Find the angle θB if it has a sway of 12.5/EI.
(Consider usual sign convention)
MFAB = MFBA = 0
By slope deflection equation, MAB = MFAB + 2EIL(2θA+θB−3Δ/L)
But the sway is towards left, so Δ is negative, 0 = 2EI/5(θB + 3×12.5/5×EI)
θB = −3×12.5/5×EI
θB = −7.5/EI
Which of the following statements are true?
1) Slope deflection method is always used for determinate structures.
2) Slope deflection method is the displacement method.
3) Modified slope deflection equation is used when one support is hinged.
4) Superposition cannot be applied in slope deflection equations.
Efflorescence of the cement is due to the excess of
Cast iron and Concrete are Brittle, but Concrete has less strength than Cast Iron.
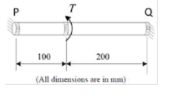
A bar of circular cross-section is clamped at ends P and Q as shown in the figure. A torsional moment T = 150 Nm is applied at a distance of 100mm from end P. The torsional reactions (Tp, T0) in Nm at the ends P and Q respectively are
T1L1 = T2L2
T1.100 = T2.200
T1 = 2T2
And, T1 + T2 = T
Hence, T1 = 100 Nm and T2 = 50Nm
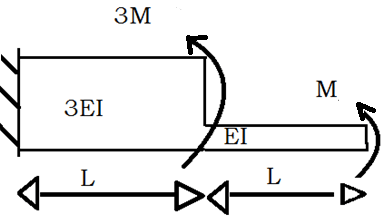
A stepped cantilever is subjected to moments as shown. The vertical deflection at free end is
Deflection of free end with respect to fixed end= Moment of M/EI diagram between the ends.
δ = M/EI × 2L × L.
δ = 2ML2/EI
A square plate of dimension L × L is subjected to a uniform pressure load p = 250 MPa on its edges as shown in the figure. Assume plane stress conditions. The Young’s modulus E = 200 GPa.
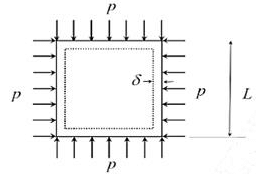
The deformed shape is a square of dimension L = 2δ. If L =2m and δ =0.001 m, the Poisson’s ratio of the plate material is ____.
A slow-moving vehicle at a speed of 84 kmph requires a clear spacing of _____ (in m) to overtake.
S = 0.7 Vb + 6 m
Vb = (84 x 1000)/(60 x 60) = 23.33 m/s
Clear space/ space headway = 16.33 + 6 = 22.33 m
The runway length after correcting for elevation and temperature is 2800m. if the effective gradient on runway is 0.8% then revised runway length will be?
= 20/100 × 2800 × 0.8 = 448
Corrected length = 2800 + 448 = 3248 m
A large hydraulic turbine is to generate 300 kW at 1000 rpm under a head of 40 m. for initial testing, a 1:4 scale model of the turbine operates under a head of 10 m. the power generated by the model (in kW) will be
Now specific speed will be same
Consider the following statements:
1) The alkalinity of the fresh water is alkaline but as time passes it becomes acidic.
2) The fresh domestic waste water is dark in colour but as time passes it becomes grey.
The colour of the waste water gets converted to dark because of
An ice cream factory has a daily discharge of the waste water at the average rate of 2400 m3/day. The waste water coming out of the factory was tested at 2% dilution and following results were obtained:
DO of aerated water = 5mg/l
DO of diluted sample = 0.5 mg/l
DO of diluted sample after 5 days = 1.4 mg/l
Deoxygenation constant = 0.1 day-1
The ultimate BOD of the sample is
4.91-1.4/2 × 100 = 175.5 mg/Id sample,
5×98+0.5×2/100 = 4.91 mg/1
DO of sample after 5 days = 3.4 mg/l
BOD5 of the sample,
4.91-1.4/2 × 100 = 175.5 mg/I
BOD5 = BODu(1-10-kdt)
BODu = 175.5/(1-10-0.5) = 256.66 mg/I
Treatment plant treating 15MLD of water requires 35mg/l of Alum. If the water has 10mg/l of alkalinity as CaCO3, find the quantity of quick lime required (tons per year as CaO)?
[Al=27, S=32, O=16, H=1, Ca=40, C=12)?
1mg of alum = 0.45mg of alkalinity as CaCO3
35mg/l of alum = 0.45 × 35 = 15.75 mg/l as CaCO3
Alkalinity to be added additionally = 15.75 – 10 = 5.75 mg/l as CaCO3
Alkaline to be added as CaO = 5.75 × 0.56 =3.22 mg/l
Total quick lime required per year = 3.22 ×15 × 365/1000
= 17.63 ton
What will be the efficiency (%) of a 20m diameter and 1m deep single state high rate trickling filter having sewage low as 4.5MLD, recirculation rate = 1.4 and BOD influent is about 185mg/l?
Efficiency,
n = 100 / (1+0.0044 (Q Yi/VF)0.5)
F = (1+R/I)/(1+0.1R/I)2 = (1+1.4)/ (1+0.1×1.4)2
= 1.87
QYi = 4.5 × 185
= 832.5 Kg
V = πD2 × 1/4 = 0.0314 ha-m
The T-alkalinity in water is 400mg/l as CaCO3 and P-alkalinity is 250mg/l as CaCO3. What will be the concentrations of OH-, CO3-2, HCO3- in mg/l respectively?
As P > 0.5T; then we have
OH- conc = 2P-T
= 2 × 250-400 = 100mg/l
CO3-2 conc = 2T-2P
= 2×400 -2×250 = 300mg/l
HCO3- conc = 0 mg/l
Note: T alkalinity is the measurement of all species of alkalinity in the water. It is the final endpoint for the alkalinity titration.
P alkalinity or Phenolphthalein alkalinity is the measurement of amount of carbonate and hydroxide using titration water samples with acid of a known concentration and using phenolphthalein indicator. It is measured down to a pH of 8.3.
For a vehicle moving on a single lane road with two-way traffic at a speed of 80 km/h, the Head light distance is _______ m.
SSD in case of Single lane with two-way traffic is Twice the SSD
SSD/HSD = 0.278 vt + v2/ (254f)
Take reaction time, t = 2.5 sec
Coefficient of friction, f = 0.35
On substituting, SSD = 55.6 + 71.99 = 127.59 = 128 m
Here HSD = 2 SSD = 256 m
For a fully developed laminar flow of water (dynamic viscosity 0.001 Pa-s) through a pipe of radius 5 cm. the axial pressure gradient is —10 Pa/m. The magnitude or axial velocity (in m/s) at a radial location of 0.2 cm is ___________ m/sec
For incompressible laminar flows through pipes velocity distribution
= 6.24m/sec.
isConverting the matrix into Echelon form,
Now since the matrix is in Echelon
Rank = Number of no-zero rows = 2
A rod of length L having uniform cross-sectional area A is subjected to a tensile force P as shown in the figure below. If the Young’s modulus of the material varies linearly from E1 to E2 along the length of the rod, the normal stress developed at the section-SS is
The normal stress across any section depends only on external force (P) & cross-section area σ = P/A is independent of young's of material.
Given that one root of the equation x3 –10x2 + 31x –30 = 0 is 5, the other two roots are
Given, x3-10x2+31x-30=
It's one root is 5, hence
(x-5) (x2-5x+6) = 0
⇒ (x-5) (x2-3x-2x+6) = 0
⇒ (x-5) (x-3)(x-2) = 0
⇒ x = 5,3,2
A steel column section ISHB 350 (width of flange is 250mm and thickness of flange 11.6mm) has to carry a factored load of 2400kN. The yield stress and the ultimate tensile stress of steel and welds are 250MPa and 410MPa respectively and partial safety factor governed by yield and ultimate tensile strength respectively are 1.10 and 1.25. The bearing strength of M25 grade concrete in limit state method of design as per IS 456:2000(inN/mm2) is
For ISHB 350 steel column,
bf = 250mm and tf = 11.6mm.
P = 2400kN, fy = 250 MPa.
For M25 grade concrete Fck = 25N/mm2
Bearing strenght of concrete = 0.45fck = 11.25N/mm2
The magnitude of bending moment at fixed end of beam shown in figure above is _________ KNm
Calculation of FEM
MFBC = - 30 × 1.2 = -36KNmMFAB
= - 120 × 4 / 8 = -60KNmFBA
= 120 × 4/8
= 60KNm
Distribution factor:
FINAL MOMENT AT FIXED END = -72KNm
If the total float of an activity in CPM has a value ‘x’ units and the head event slack has a value ‘y’ units, find out the value of the independent float if the tail event slack is 10. ?
Reason: Free float = Total float – Head event slack
Free float =x-y
We know that,
Free float = Independent float + Tail event slack
x-y = Independent float + 10
Then, Independent float = x-y-10
The data given below pertain to the design of a flexible pavement are
Initial traffic = 1213 cvpd
Traffic growth rate = 8 per cent per annum
Design life = 12 years
Vehicle damage factor = 2.5
Distribution factor = 1.0
The design traffic in terms of million standard axles (msa) to be catered would be
Cumulative number of standard axle load
A = Number of commercial vehicle or initial traffic = 1213 cvpd
r = Traffic growth rate = 8% per annum
n = design life = 2 years
f = vehicle damage factor = 2.5
The velocity potential function in a two dimensional flow field is given by ∅ = x2-y2.The magnitude of velocity at point (1, 1) is
The flow in a rectangular channel is subcritical. If width of the channel is reduced at a certain section, the water surface under no–choke condition will
In the subcritical region of flow for a given specific energy, as the discharge per unit width q is increased due to reducing width at the section, the depth of flow will decrease.
Therefore the water surface drops at a downstream section.
Alternately
∴ q1 > q2
From the discharge diagram, it can be seen that, for subcritical flow as q increases, depth decreases.
Therefore at the reduced section, depth decreases.
Given, three spans each of length 2 m.
What will be the change in rotation of θB if the middle span settles by 4/EI.
A thin gas cylinder with an internal radius of 100 mm is subject to an internal pressure of 10 MPa. The maximum permissible working stress is restricted to 100 MPa. The minimum cylinder wall thickness (in mm) for safe design must be
We know that the σ1 = pd/2t
Putting values, 100 = 10×2×100/2×t
⇒ t = 100 mm
In a preliminary survey a line of level was run from a bench mark of RL 454.650m and following readings are obtained. fly levelling was done till last position of the instrument
2.545,1.365,3.865,2.945,2.670,1.885,1.125
From the last position of the instrument five pegs at 20m interval and to be set out ib an uniformly rising gradient of 1 in 40. The first peg is to have a Rl of 455.110 Find the staff reading for the fourth peg.
What is the value of friction factor, if the diameter of pipe is 100 cm and roughness height is 0.25 cm?
1/√f = 2 log (R/K) + 1.74
f = 0.0248
The specific gravity & weight proportion of aggregate & bitumen are as under for the preparation of Marshall Mix design. The volume & weight of one marshal specimen was found to be 600 cc and 1000 gm. Assuming absorption of bitumen in aggregate is zero. The percentage air void is ________%.
The driver of a vehicle travelling 75 km/hr up a gradient requires 10 m less to stop after he applied brakes, as compared to a driver travelling at the same speed, down the same gradient given, f = 0.40 what is the present gradient?
Braking distance up the gradient
In a pipe of diameter 20 cm, a liquid of density 800 kg/m3 is flowing with a discharge of pipe 350 l/sec and friction factor is estimated as 0.0085. If viscosity of liquid is 2.9×10-4 Ns/m2 and assuming pipe is in smooth turbulent flow region then shear velocity will be
Given ; d = 20 cm ; ρ = 800 kg/m3 ; Q = 350 l/sec = 0.35 m3/sec
f = 0.0085 ; µ = 2.9 × 10–4 Ns/m2
V× = 0.363 m/sec
What are the coordinates of the center of Mohr’s circle for an element subjected to two mutually perpendicular stresses one tensile of magnitude 80MPa and other compressive of magnitude 50MPa?
σx = 80 MPa,
σy = -50 MPa
Co-ordinates of center of Mohr’s circle =[ ½( σx + σy),0]
= [(30/2),0]
= (15,0)
Determine the deoxygenation coefficient at 37˚C, when the self-purification factor of a river is 4.25 and the rate at which re-oxygenation happens is 0.3 per day at a standard temperature of 20˚C.
When two mutually perpendicular principal stresses are unequal but alike, the maximum shear is represented by __________.
It's half of the dia. Shows the maximum stress at angle is 45 so radius of the circle shows the maximum stress.
To lift water from a ground reservoir to an overhead tank of capacity 0.90 cu.m. capacity, what is the appropriate H.P. of centrifugal pump to be installed, such that the OHT gets filled up in 1 hour. Consider the difference in water level as 50m. Assume the efficiency as 65%.
Total head, H = 4m + 50m = 54m
Brake Horsepower of Pump (in H.P.) = wQH/75n
In a typical load cycle over a component the maximum and minimum stresses of 245 N/m2 and 132 N/m2 are indicated respectively. Therefore the variable stress induced is _________.
σmin = 132 N/m2
The variable stress is given by,
Variable stress, σv = σmax − σmin/2 = 245−132/2 = 56.5MPa
The plastic limit of soil is 25%. Ir = 6%, where the soil is dried from its state at plastic limit, the volume change is 25% of its value at plastic limit. The corresponding change from liquid state to dry state is 30% of its volume at liquid limit. Determine the shrinkage ratio:
Now equating the slopes:
A cantilever beam of square cross section having depth 600 mm and span 8 m is subjected to a uniformly distributed load of magnitude 8.25 kN/m2. The stress generated at a distance equal to 2m from the free end and at a depth of 250 mm from top will be
Bending moment at a distance equal to 2 m =
Since the bending moment is hogging in nature, stresses above the neutral axis will be tensile in nature.
The necessary and sufficient condition for a surface to be called as a free surface is
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress, such as the boundary between two homogeneous fluids, for example liquid water and the air in the Earth's atmosphere. Unlike liquids, gases cannot form a free surface on their own. So, no stress should be acting on it.
|
27 docs|296 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
27 docs|296 tests
|
Download free EduRev App
Related content with Practice Test: Civil Engineering (CE)- 12
|
|
|
|
Related tests with Practice Test: Civil Engineering (CE)- 12
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
