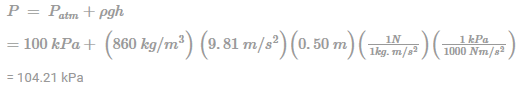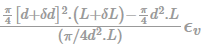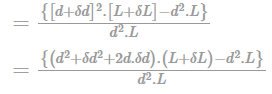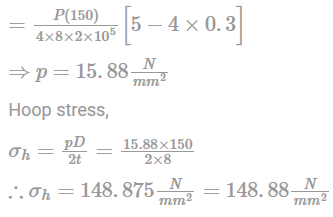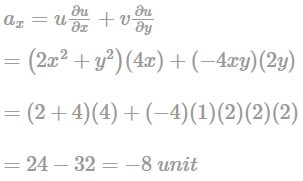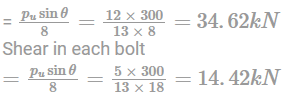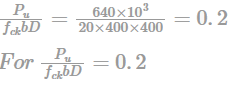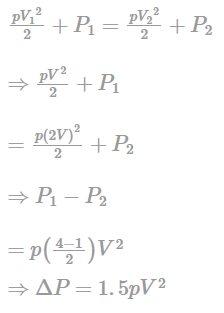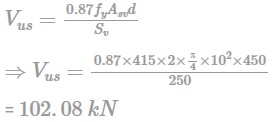Practice Test: Civil Engineering (CE)- 15 - Civil Engineering (CE) MCQ
30 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Practice Test: Civil Engineering (CE)- 15
For a > b, if a + b = 5 and ab = 6, then the value of (a2 - b2) is
In the following question, out of the given alternatives, select the word opposite in meaning to the given word.
Inevitable
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the difference between the expenditure made by a university for the publication of journals and psychology?
Total Expenditure : Rs. 60 Lacs
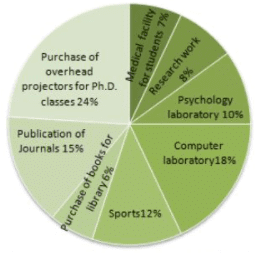
Expenditure of funds By University for various purposes

In the following questions groups of four words are given. In each group, one word is spelt.
Find the correctly spelled word.
Select the most appropriate antonym of the given word.
INNOCUOUS
Choose the most appropriate word from the options given below to complete the following sentence.
Communication and interpersonal skills are ......... important in their own ways.
In the following question, some of the sentences have errors and some have none. Find out which part of a sentence has an error. The number of that part is the answer. If there is no error, your answer is (4) i.e., No error.
We requested the watchman (1)/ to clean up the basement (2)/ so that the children had enough space to play (3)/ No error (4)
The Palghat Gap (or Palakkad Gap), a region about 30 km wide in the southern part of the Western Ghats in India, is lower than the hilly terrain to its north and south. The exact reasons for the formation of this gap are not clear. It results in the neighbouring regions of Tamil Nadu getting more rainfall from the South West monsoon and the neighbouring regions of Kerala having higher summer temperatures.
Q. What can be inferred from this passage?
It takes 30 minutes to empty a half-full tank by draining it at a constant rate. It is decided to simultaneously pump water into the half-full tank while draining it. What is the rate at which water has to be pumped in so that it gets hilly filled in 10 minutes?
While receiving the award, the scientist said, "I feel vindicated”. Which of the following is closest in meaning to the word ‘vindicated’?
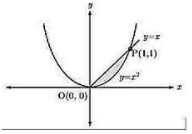
The area enclosed between the parabola y = x2 and the straight line y = x is
Which of the following statement is INCORRECT?
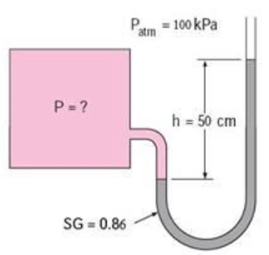
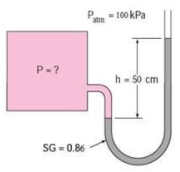
A manometer is used to measure the pressure in a tank. The fluid used has a specific gravity of 0.86, and the manometer column height is 50cm, as shown in figure If the local atmospheric pressure is 100kPa, calculate the absolute pressure within the tank.
Take the standard density of water to be 1000kg/m3.
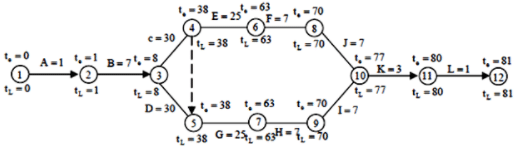
A construction project consists of twelve activities. The estimated duration (in days) required to complete each of the activities along with the corresponding network diagram is shown below.
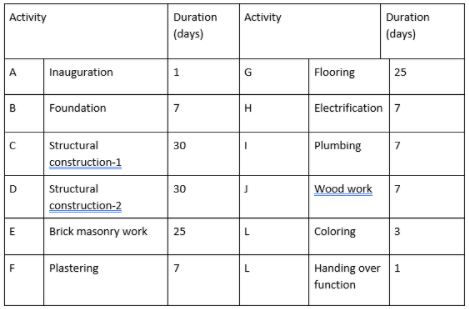
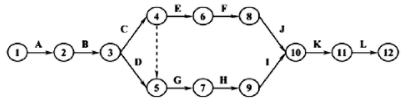
Total floats (in days) for the activities 5-7 and 11-12 for the project are, respectively,
A cylindrical shell 1000 mm long, 150 mm internal diameter, having a thickness of 8 mm is filled with a fluid at atmospheric pressure. An additional 25000 mm3 of fluid is pumped into the cylinder, then the hoop stress-induced will be ___________ N/mm2[E=2×105 N/mm2 and μ=0.3]
There is a free overfall at the end of a long open channel. For a given flow rate, the critical depth is less than the normal depth. What gradually varied flow profile will occur in the channel for this flow rate?
For a given PERT activity, the standard deviation of the time needed to complete an activity is 3. If the optimistic time and the most likely time required to complete this activity are 8 and 12 minutes respectively. Find out the expected time in order to complete this activity.
The concentration of Sulfur Dioxide (SO2) in the ambient atmosphere was measured as 30 µg/m3. Under the same conditions, the above SO2 concentration expressed in ppm is ___________.
Given: (P/(RT) = 41.6 mol/m3; where, P = Pressure; T = Temperature; R – universal gas constant; Molecular weight of SO2 = 64.
A steady, incompressible flow is given by:
u = 2x2 + y2 and v= -4xy , What is the convective acceleration along x-direction at point (1, 2)
A two-faced fair coin has its faces designated as head (H) and tail (T). This coin is tossed three times in succession to record the following outcomes: H, H, H. If the coin is tossed one more time, the probability (up to one decimal place) of obtaining H again, given the previous realizations of H, H and H, would be_____.
The function f(x) = 2x3 – 3x2 – 36x + 2 has its maxima at
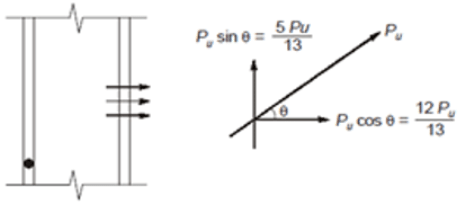
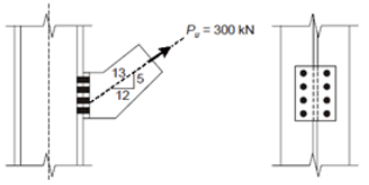
The ratio of tension and shear force in each bolt of the joint, as shown in figure, is
Three values of x and y are to be fitted in a straight line in the form y = a + bx by the method of least squares. Given : N=3, ∑x = 6, ∑y = 21, ∑x2 = 14 and ∑xy = 46, the values of a and b are respectively.
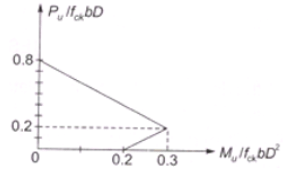
A RC column of square cross-section (400×400mm2) has its column load-moment interaction diagram as shown in figure below.
At two points 1 and 2 in a pipeline the velocities are V and 2V, respectively. Both the points are at the same elevation. Both the points are at the same elevation. The fluid density is ρ. The flow can be assumed to be compressible, inviscid, steady and irrotational. The difference in pressures P1 and P2 at points I and 2 is
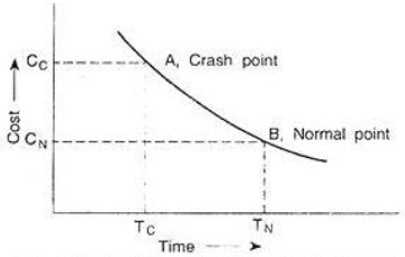
In a network, a project activity has normal cost and normal duration of Rs. 400 and 8 days respectively. The same activity has crash cost and crash duration of Rs. 800 and 6 days. The crash cost slope of activity is;
Precast concrete pile of size 50 cm × 50 cm is to be driven into clay strata. The unconfined compressive strength of which is 110 kN/m2. Then the length required to carry a safe working load of 500 kN with FOS = 3 and α = 0.6 is _______ m.
An RC beam of rectangular cross-section has 250 mm width and 450 mm effective depth. Vertical stirrups 2-legged 10 mm diameter are provided at a spacing of 250 mm centre to centre and assume design shear strength of concrete is 0.6 MPa. The total shear capacity (in kN) of the section is
[Use Fe 415 grade steel for stirrups]
The command area of a channel is 4000 hectares. The intensity of irrigation of a crop is 70% and it requires 60 cm of water in 15 days, when the effective rainfall is recorded as 15 cm during that period, then the duty at the head of the channel is _________ ha/cumec.
[Assume total losses as 15%]
A horizontal water jet with a velocity of 10 m/s and cross-sectional area of 10mm2 strikes a flat plate held normal to the flow direction. The density of water is 1000kg/m3. The total force on the plate due to the jet is
|
31 docs|280 tests
|
|
31 docs|280 tests
|