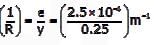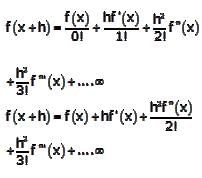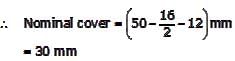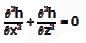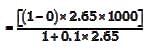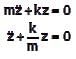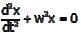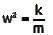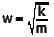Practice Test: Gate Civil Engineering(CE) 2019 Paper: (Session I) - GATE MCQ
30 Questions MCQ Test - Practice Test: Gate Civil Engineering(CE) 2019 Paper: (Session I)
They have come a long way in _______ trust among the users.
The CEO’s decision to quit was as shocking to the Board as it was to __________.
The lecture was attended by quite _________ students, so the hall was not very___________.
If E = 10; J = 20; O = 30; and T = 40, what will be P + E + S + T?
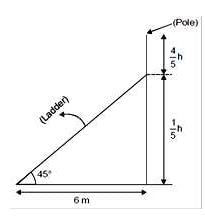
On a horizontal ground, the base of straight ladder is 6m away from the base of a vertical pole. The ladder makes an angle of 45° to the horizontal. If the ladder is resting at a point located at one-fifth of the height of the pole from the bottom, the height of the pole is _____meter.
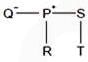
P, Q, R, S and T are related and belong to the same family. P is the brother of S. Q is the wife of P. R and T are the children of the siblings P and S respectively. Which one of the following statements is necessarily FALSE?
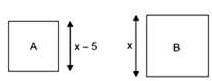
A square has sides 5cm smaller than the sides of a second square. The area of the larger square is four times the area of the smaller square. The side of the larger square is ________cm.
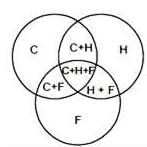
In a sports academy of 300 people, 105 play only cricket, 70 play only hockey, 50 play only football, 25 play both cricket and hockey, 15 play both hockey and football and 30 play both cricket and football. The rest of them play all three sports. What is percentage of people who play at least two sports?
The increasing interest in tribal characters might be a mere coincidence, but the timing is of interest. None of this, though, is to say that the tribal hero has arrived in Hindi cinema, or that the new crop of characters represents the acceptance of the tribal character in the industry. The films and characters are too few to be described as a pattern.
Q. Who does the word ‘arrived’ mean in the paragraph above?
The new cotton technology, Bollgard-II, with herbicide tolerant traits has developed into a thriving business in India. However, the commercial use of this technology is not legal in India. Notwithstanding that, reports indicate that the herbicide tolerant Bt cotton had been purchased by farmers at an average of Rs 200 more than the control price of ordinary cotton, and planted in 15% of the cotton growing area in the 2017 Kharif season.
Q. Which one of the following statements can be inferred from the given passage?
In a soil specimen, the total stress, effective stress, hydraulic gradient and critical hydraulic gradient are σ, σ’, i and ic, respectively. For initiation of quicksand condition, which one of the following statement is TRUE?
Assuming that there is no possibility of shear buckling in the web, the maximum reduction permitted by IS 800-2007 in the (low-shear) design bending strength of a semi-compact steel section due to high shear is
The coefficient of average rolling friction of a road is fr and its grade is +G%. If the grade of this road is doubled, what will be the percentage change in the braking distance (for the design vehicle to come to stop) measured along the horizontal (assume all other parameters are kept unchanged)?
A circular duct carrying water gradually contracts from a diameter of 30cm to 15cm. The figure (not drawn to scale) shows the arrangement of differential manometer attached to the duct.
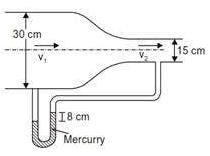
When the water flows, the differential manometer shows a deflection of 8cm of mercury (Hg). The values of specific gravity of mercury and water are 13.6 and 1.0, respectively. Consider the acceleration due to gravity, g = 9.81 m/s2. Assuming frictionless flow, the flow rate (in m3/s, round off to 3 decimal places) through the duct is __________.
A concentrated load of 500 kN is applied on an elastic half space. The ratio of the increase in vertical normal stress at depths of 2m and 4m along the point of the loading, as per Boussinesq’s theory, would be _______.
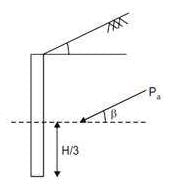
A retaining wall of height H with smooth vertical backface supports a backfill inclined at an angle β with the horizontal. The backfill consists of cohesionless soil having angle of internal friction ϕ. If the active lateral thrust acting on the wall is Pa which one of the following statements is TRUE?
In a rectangular channel, the ratio of the velocity head to the flow depth for critical flow condition, is
The probability that the annual maximum flood discharge will exceed 25000 m3/s, at least once in next 5 years is found to be 0.25.The return period of this flood event (in years, round off to 1 decimal place) is _____________.
The interior angles of four triangles are given below:
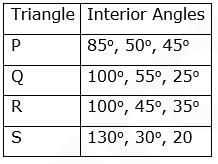
Q. Which of the triangles are ill-conditioned and should be avoided in Triangulation surveys?
A catchment may be idealised as a rectangle. There are three rain gauges located inside the catchment at arbitrary locations. The average precipitation over the catchment is estimated by two methods: (i) Arithmetic mean (PA) and (ii) Thiessen polygon (PT).
Q. Which of the following statements is correct?
An isolated concrete pavement slab of length L is resting on a frictionless base. The temperature of the top and bottom fibre of the slab are Tt and Tb, respecitvely. Given: the coefficient of thermal expansion = α and the elastic modulus = E. Assuming Tt > Tb and the unit weight of concrete as zero, the maximum thermal stress is calculated as
For a given loading on a rectangular plain concrete beam with an overall depth of 500 mm, the compressive strain and tensile strain developed at the extreme fibers are of the same magnitude of 2.5 × 10-4. The curvature in the beam cross-section (in m-1, round off to 3 decimal places), is __________.
For a small value of h, the Taylor series expansion of f(x + h) is
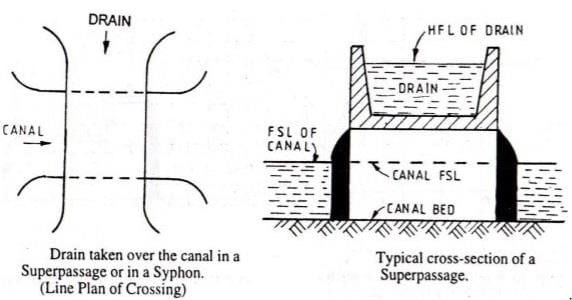
If the path of an irrigation canal is below the level of a natural stream, the type of cross drainage structure provided is
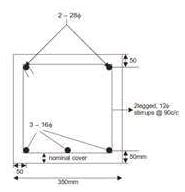
In the reinforced beam section shown in the figure (not drawn to scale), the nominal cover provided at the bottom of the beam as per IS 456–2000, is
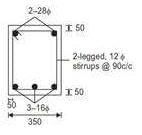
All dimensions are in mm
Consider a two-dimensional flow through isotropic soil along x-direction and z-direction. If h is the hydraulic head, the Laplace’s equation of continuity is expressed as
A soil has specific gravity of its solids equal to 2.65.The mass density of water is 1000 kg/m3. Considering zero air voids and 10% moisture content of the soil sample, the dry density (in kg/m3, round off to 1 decimal place) would be _______.
Which one of the following is correct?
A plane truss is shown in the figure (not drawn to scale).
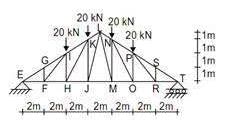
Q. Which one of the options contains ONLY zero force members in the truss?
A simple mass-spring oscillatory system consists of a mass m, suspended from a spring of stiffness k. Considering z as the displacement of the system at any time t, the equation of motion for the free vibration of the system is The natural frequency of the system is



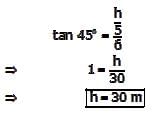
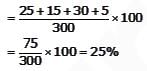
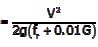
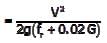

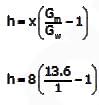
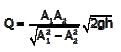
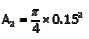

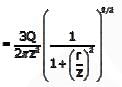
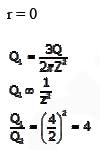
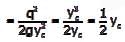
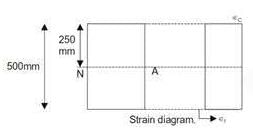
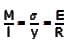
 Curvature of beam cross-section
Curvature of beam cross-section