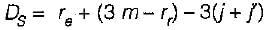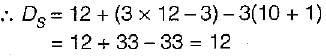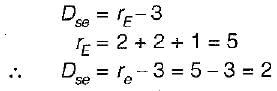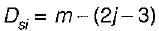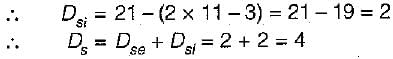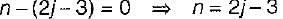Test: Determinacy & Indeterminacy -1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Test: Determinacy & Indeterminacy -1
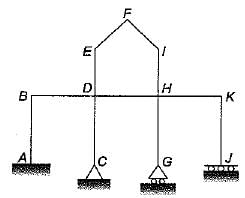
Total degree of indeterminacy (both internal and external) of the plane frame shown in the given figure is

If there are m unknown member forces, r unknown reaction components and j number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Degree of kinematic indeterminacy of a pin jointed plane frame is given by where j is number of joints and r is reaction components.
A pin-jointed plane frame is unstable if where m is number of members r is reaction components and j is number of joints
The degree of static indeterminacy of a pin- jointed space frame is given by
The degree of kinematic indeterminacy of a pin-jointed space frame is given by
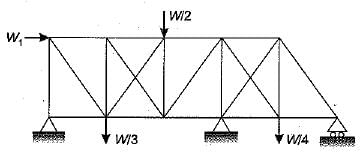
The degree of static indeterminacy of the pin- jointed plane frame shown in figure is
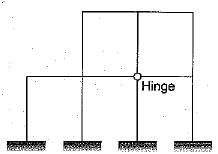
The portal frame as shown in the given frame is statically indeterminate to the
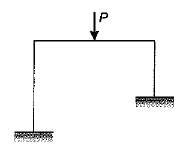
A perfect plane frame having n number of members and j number of joints should satisfy the relation
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is
|
31 docs|280 tests
|
|
31 docs|280 tests
|