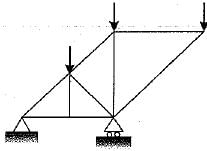
Test: Determinacy & Indeterminacy -2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Test: Determinacy & Indeterminacy -2
If 4 reactions are acting on a beam, then the system is:-
A prismatic beam is shown in the figure given below.
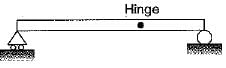
Consider the following statements:
1. The structure is unstable.
2. The bending moment is zero at supports and internal hinge.
3. It is a mechanism,
4. It is statically indeterminate.
Which of these statements are correct?

Consider the following statements:
1. The structure is unstable.
2. The bending moment is zero at supports and internal hinge.
3. It is a mechanism,
4. It is statically indeterminate.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
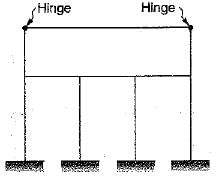
The rigid-jointed frame shown in the figure is
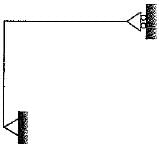

What is the degree of static indeterminacy of the plane structure as shown in the figure below?
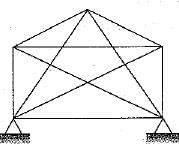
Consider the following statements:
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacy
Which of these statements is correct?
Which one of the following structures is statically determinate and stable?
How is a truss, which undergoes rigid body translation for an arbitrary load, classified as?
The degree of static indeterminacy of the rigid frame having two internal hinges as shown in the figure below is

What is the total degree of indeterminacy both internal and external of the plane frame shown below?
|
31 docs|280 tests
|
|
31 docs|280 tests
|